In this essay I want to start an exploration into General Relativity in the context of the Big Bang Hypernova Hypothesis. Until now, I have particularly focused my arguments upon the two output jets each travelling in polar opposite directions with respect to the other. However a hypernova also gives birth to a rotating black hole and it is upon this aspect I now wish to concentrate.
Now it is important to point out that I would consider my understanding of General Relativity to be rather shallow. Since having the idea that led to the development of my hypothesis, over the last number of years, I’ve been building up an understanding and appreciation for the fundamental ideas behind General Relativity as I let knowledge seep into my bones. So am I learning those critical insights, thought experiments and constructs that allow me to visualise it within my mind’s eye. A talent developed from an obsession of wanting to model and understand the geometry of waves, whirlpools and turbidites within a computational fluid dynamics algorithm. [1]
So on the one hand I feel like a new comer to the mathematics of General Relativity; it being its own academic world of literature and publications. But it is familiar being a system of partial differential equations, like the Navier-Stokes equation, but with the subtlety and complexity dialled up. I also understand how using words such as “open” and “closed” alone can be the source of massive debate; particularly with respect to describing our universe as being causally closed. So in reading this essay please bare this in mind.
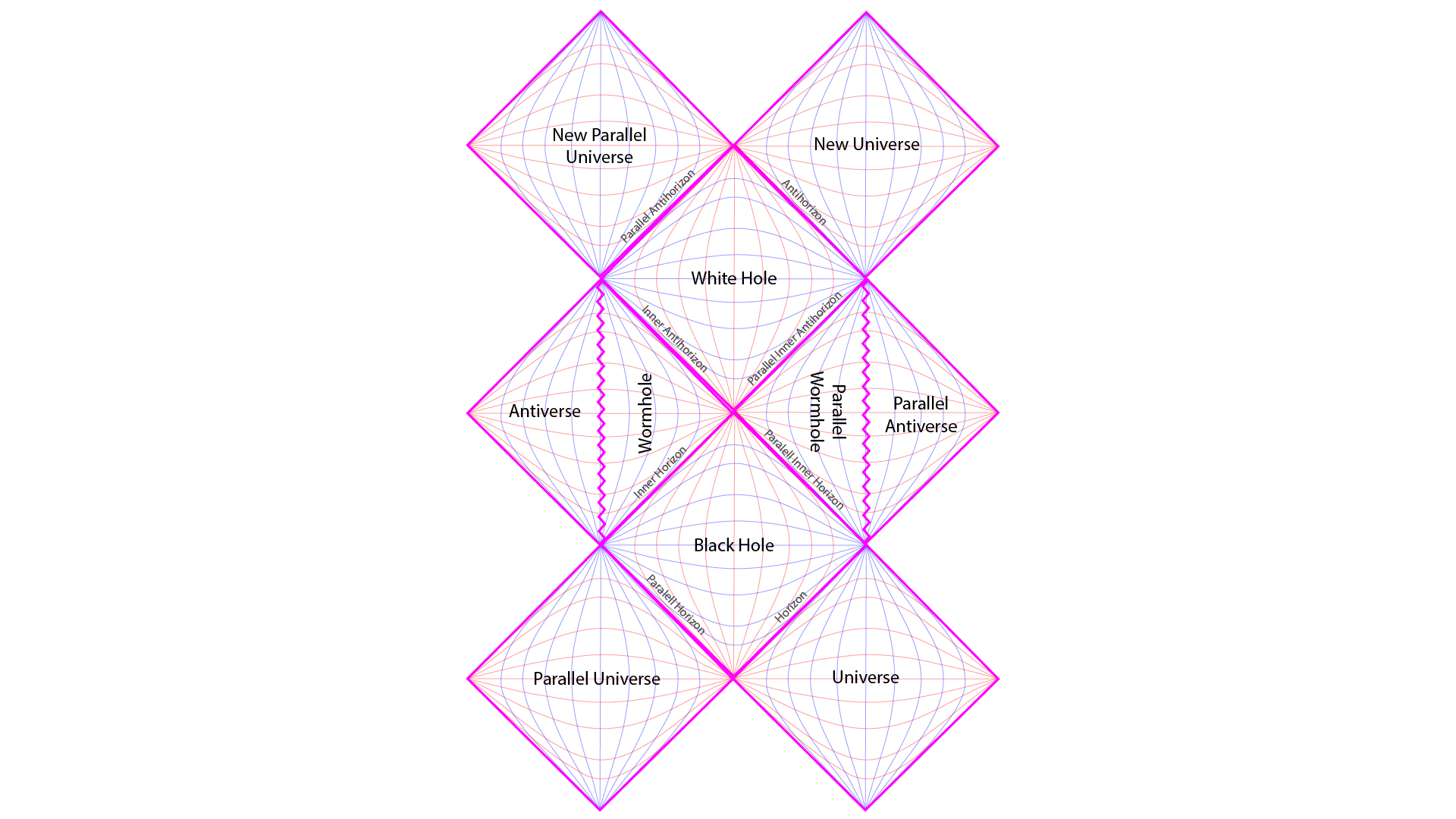
Maximally extended Penrose Diagram of a rotating black hole. Two parallel universes are connected to the given black hole. Rotation, via the Kerr metric, shows how inside the black hole the path of causality takes us through the wormhole in its interior. This wormhole in turn leads to a white hole which exits out into either one of two new parallel galaxies. [2]
The main point that I am trying to communicate comes as a logical consequence of the Big Bang Hypernova Hypothesis in combination with a maximally extended Penrose Diagram of a rotating black hole. So by my hypothesis, a rotating black hole is born in the Superverse which in turn gives birth to a white hole in the same location. This white hole becomes the source well spring of spacetime that gives birth to our universe. Thus our universe inflates like a balloon to occupy a subset of the volume of the Superverse. [2]
As fractal geometry is the cosmological principle then it means the same pattern of behaviour seen on the larger scale is also found at the smaller scale, that being scale-invariance. So if this version of events, that is my Big Bang Hypernova Hypothesis, has any validity then it would mean a rotating black hole inside our universe should have a similar pattern of behaviour. For instance, there should be two massive balloon voids adjacent and aligned with the poles of the supermassive black hole at the heart of the Milky Way galaxy.
Also for a long time now, I have tried to picture how or what it would look like if I could see our universe from the outside as it expands into the volume of the Superverse. I imagine that which to us is both the unidirectional arrow of time and the force of gravity as being equivalent to the electro-magnetic force of the Superverse, on the next scale up.
So a gravitational wave in our universe would be like an electrical wave within the Superverse. Certainly such interactions are some of the most extreme high energy events that happen inside our own universe. For instance, the merging of two black holes or neutron stars.; never mind hypernovae. These high energy events inside our universe would also be high energy events that emit high energy “Super-photons” out into the enclosed vacuum space of the Superverse. [3]
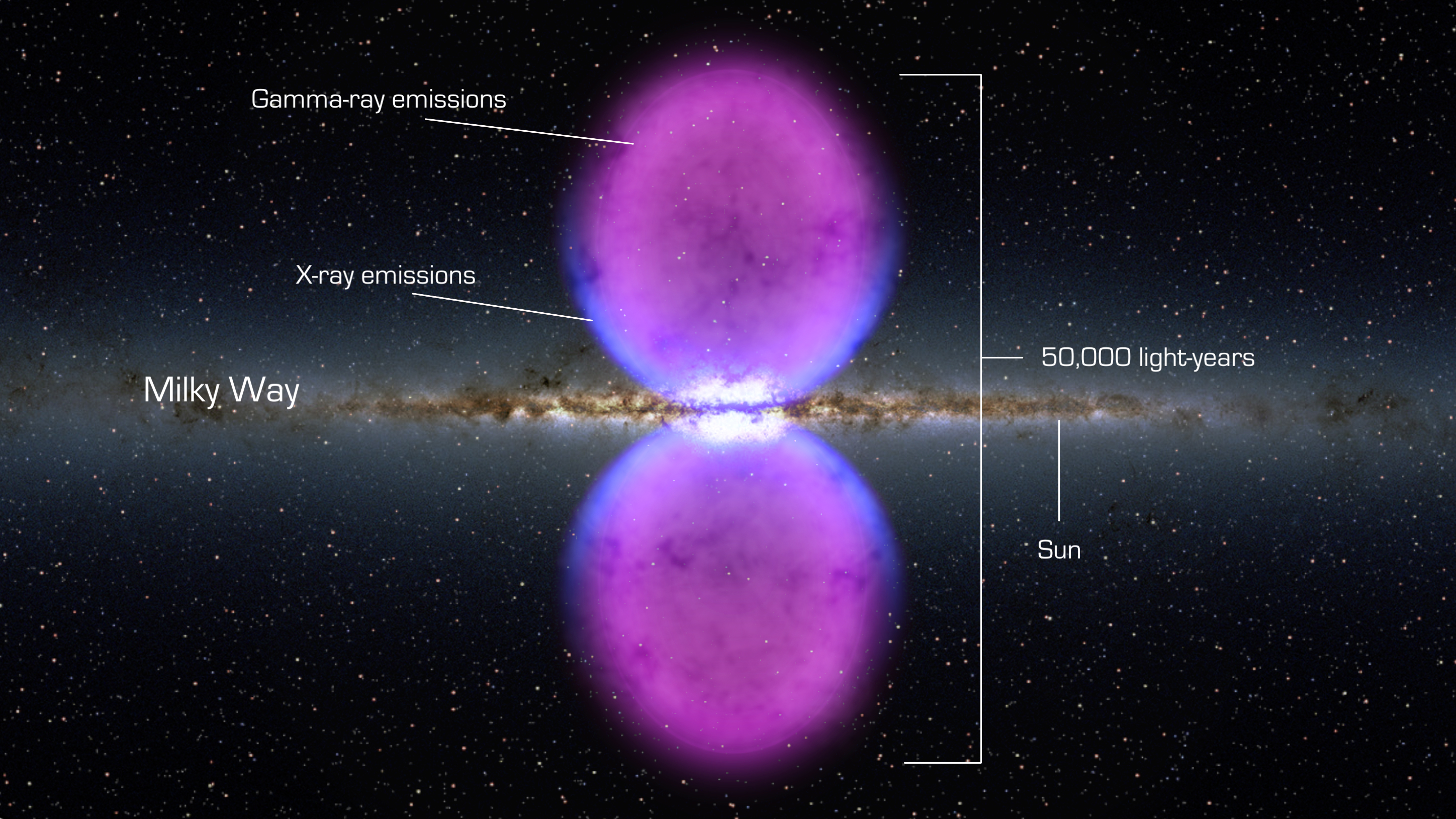
From end to end, the newly discovered gamma-ray bubbles extend 50,000 light-years, or roughly half of the Milky Way's diameter, as shown in this illustration. Hints of the bubbles' edges were first observed in X-rays (blue) by ROSAT, a Germany-led mission operating in the 1990s. The gamma rays mapped by Fermi (magenta) extend much farther from the galaxy's plane. Credits: NASA's Goddard Space Flight Center [4]
But what would that interaction look like inside our own universe? To whit I am eternally in the debt of the Fermi Gamma-ray Space Telescope team. Not just for those Gamma-Rays Burst observations but also for giving the Big Bang Hypernova Hypothesis its greatest bastion yet; namely Fermi Bubbles. And so, we can identify a key component of nature in seeing how one universe can contain another in order to understand the recursive fractal pattern of nature itself. [5]
In order to start our deep dive exploration into all of this let us start at the beginning.
The Big Bang Theory itself began following the observation, particularly by Georges Lemaître, that galaxies in general are moving away from one another. Lemaître, using Einstein’s equations of General Relativity, found that if the clock on the universe was reversed then those galaxies would move back towards each other. The ultimate conclusion being that the universe as a whole was born in the event that later came to be called the “Big Bang”; when Fred Hoyle coined the term.
I have the feeling that many cosmologists dislike the name Big Bang because of the notion that it was like a big explosion such as a hypernova. The reason being that it miscommunicates a very important notion of the classical Big Bang Theory as described by quantum mechanics. The notion is that at the moment of the Big Bang everything that exists, all matter and energy, was contained inside an infinitely small but infinitely dense point, the singularity.
It is the inflationary expansion of this the Big Bang singularity that gives the classical theory its story. And a very important part of that story is that all of spacetime is contained inside this expanding bubble. It does not consider it as a bubble expanding to occupy an existing volume because there is no existing volume outside of this bubble.
The Big Bang Hypernova Hypothesis scraps this notion in giving definition to the Superverse. The Superverse acts and behaves, following the same dynamic patterns, in a manner similar to how our own universe does. Or rather our universe inherits the characteristics of our parent Superverse. However it does this at a much greater scale.
We can give ourselves to permission to picture the Superverse as such because fractal geometry is the cosmological principle and self-similar patterns repeat themselves irrespective of scale. We get the impression of the actual difference in scale in seeing a single star of the Superverse, the MacLean, in the spherical shadow of the Boötes Supervoid.
Like a balloon being inflated and blown up inside a closed room the Big Bang Hypernova Hypothesis imagines our universe being inflated inside a closed Superverse. As the balloon fills up with air it expands and comes to occupy a subset of the volume inside the closed room. The volume of the room is in effect a superset of the volume occupied by the inflated balloon. So too is the volume occupied by the Superverse a superset of the volume occupied by our universe and hence the given name.
Now this is in opposition to the established viewpoint of the classical Big Bang Theory where there is no closed room. It doesn’t exist because the classical view is nothing exists outside the bubble that is our expanding universe. A total paradox given that something must have existed that led to the Big Bang event in the first place. But how can you have cause and effect when our vision of time cannot see beyond the event horizon of the Big Bang singularity? Well firstly we need to recognise exactly what that event horizon is and why it came into existence.
In trying to define the problem I find I need to first describe two binary states of spacetime that directly arise from the study of Black Holes and General Relativity.
The first is a “causally and continuously closed vacuum space” which, I guess, can be most accurately described as a Lorentzian manifold. In English, it is the fabric of spacetime as described by Einstein’s equations of General Relativity. It is the volume of empty space for a given unidirectional arrow of time.
As an analogy to Einstein’s Theory of General Relativity we view spacetime as being like a cloth fabric that can be deformed into different shapes. Mass causes the fabric of spacetime to deform inwards like a ball falling onto a cloth. In inverse, dark energy causes the fabric of spacetime to deform outwards. This is analogues to a ball thrown upwards hitting the cloth on the other side.
Another analogy comes from the observation that the universe behaves like a superfluid. This is particularly given form by Superfluid Vacuum Theory. So let us imagine a MacLean in the Superverse whose position lies directly in the path of flow of our expanding universe. The MacLean being a physical object in the Superverse causes our fluidic Jet-A-Verse to flow around it.
Seeing spacetime as a flat cloth the MacLean, being composed of dark energy to us, deforms the fabric outwards pushing galaxy clusters aside as the volume of our expanding universe flows around the volume of the MacLean. Thus we observe a big spherical void of nothingness such as the Bootes Void around whose boundaries galaxies flow; mostly in the same general direction.
A very critical point I believe is that the vacuum is outside the volume occupied by the event horizon of any particle. This point comes from thinking both about Pauli’s exclusion principle coupled with the Archimedes principle particularly in light of how I describe the formation of the Boötes Supervoid within our own universe.
However, in our picture we have manifolds growing inside manifolds. Or rather, Fermi bubbles expanding inside our universe which follows the same pattern, on the next scale up, as to how our universe continues to expand inside the Superverse. To separate them I specifically choose the words “causally and continuously closed”, for reasons we will expand upon. The Lorentzian manifold itself equates to the words “vacuum space”.
The first reason in using the words “causally and continuously closed” comes from the choose of appropriate boundary conditions in Penrose’s Singularity Theorem: “there exists a trapped surface of spacetime”. As we’ll see it was this critical insight by Roger Penrose that led to the formulation of the Penrose-Hawking Singularity Theorems and for which Penrose has just been awarded the 2020 Nobel Prize in Physics. [6]
Lecture about the history of black holes and singularities by Oxford Mathematics in which Roger Penrose explains his Singularity Theorem. [6]
The second reason, specifically in using the word “closed”, comes from a study of the spectra of the Planck CMB data showing a positive curvature with a 99% confidence level. However there is a level of subtlety here because the CMB data shows us a universe that is both flat and closed. In thinking about my first computational model the way the jet expands laterally from the direction of the jet produces a series of concentric rings whose conic sides are flat. [7] [8]
Our universe is closed being a “trapped surface of spacetime” following Penrose’s Singularity Theorem. How this is exactly the case is one of the main focal points of this essay. The shape of the Superverse into which our universe is expanding, on the other hand, is on average mostly flat. Just as our universe, into which the Fermi Bubble expands, is mostly flat. Those areas inside our universe which are not flat are occupied by astronomical bodies with mass such as stars. Areas in the Superverse, like the Boötes MacLean, where there is a concentration mass have a positive curvature upon the fabric of the Superverse. [9]
The third reason, specifically in using the word “continuously”, comes from this study of gamma-ray bursts by the Fermi Telescope. If spacetime was discrete at the Planck scale then the arrival between the photons with the shortest and longest wavelengths would have been longer. In the context of quantum mechanics being discrete I am drawn to the mathematics of spherical harmonics. [10] [11] [12]
The fourth reason that makes me say “causally closed” comes from thinking about an object falling into a black hole. From the relative frame of reference an outside observer will see an object falling towards a black hole but never will they see it fall through the event horizon. This is because the metric of spacetime becomes increasingly smaller until at the event horizon it becomes zero; the paradox of Zeno’s arrow. In effect the surface area and its associated entropy grows. Vice versa, an object cannot fall back into a white hole. It is the conformally infinite boundary limits that separates verses within the context of a maximally extended Penrose diagram. [13]
In continuing to think about an object that crosses an event horizon of a black hole we now encounter the second type of spacetime geometry. For a long time now I have been trying to imagine what it would be like to fall inside an electron or a quark. In my CPT-Symmetry film I try to describe one version of this idea based on the ideas of negative mass with a reverse arrow of time. However the more I have dug the more I believe this not to be the case.
What I do believe to be the case comes in how the dimensions of space and time interchange their roles upon a Penrose diagram as we cross over the event horizon. How this is, I find, is best understood from the relative frame of reference of the object which is free-falling in towards a black hole. From the prospectus of this reference frame the object is at rest. However when witnessed from a reference frame orbiting the black hole the object is seen to be accelerating towards the black hole as it follows the increasing curvature of spacetime down towards the black hole’s central point.
The object with respect to the outside observer is seen accelerating to speeds approaching the speed of light. By Special Relativity we know the closer an object moves towards the speed of light the greater the time dilation between the object’s reference frame and the outside observer’s frame of reference. A second for the object becomes a week, a month, a year to the outside observer.
Ultimately at the event horizon the object at rest is free-falling in towards the black hole at the speed of light. Thus the unidirectional passage of time comes to a halt and a metre has zero length at the event horizon. For the outside observer the object will never be seen to reach the event horizon as that event only happens in the far off infinite future. What the outside observer actually sees is light from the object becoming ever increasingly red-shifted and fainter until it vanishes forever over the observational horizon that is the black hole’s event horizon.
Another way to look at this comes is in seeing the metric of length become smaller and smaller as we approach the black hole. A metre is defined by how far a photon travels in a vacuum for a given length of time. But that length in the metric becomes scaled down and down until it is nothing at the event horizon. In fact, this observation that the metric of one vacuum space being scaled down is what I would describe as the critical function that drives the fractal pattern of recursion. After all a black hole scales down one reality in order to create a new universe at a much s maller scale; which is the new and unique part that we are unearthing and discovering in the context of the Big Bang Hypernova Hypothesis. [14]
In totality both the unidirectional passage of time and the metric of space, length of a metre, are reduced further and further the closer we are to the event horizon. Then at the event horizon itself the metric of both space and time are reduced to zero. But from the relative prospectus of a free-falling object it sees itself both approaching and crossing over the event horizon. So what happens to the object once across the event horizon and how do we picture such a thing?
PBS Space Time’s episode explaining the interchange in a role a dimension plays when falling inside the event horizon of a black hole.
The proposed solution, or interpretation, is reflected in the Penrose diagram in how the role of a given dimension changes. A spatial dimension transitions into becoming a temporal one. And vice versa, the unidirectional arrow of time is flipped into becoming a unidirectional spatial dimension. It is unidirectional because the only possible direction of travel is now downwards towards the gravitational singularity.
Thus beyond the event horizon we find ourselves in a verse where causality is three-dimensional but only with a single unidirectional spatial path. In effect, the continuous vacuum space of the larger verse is effectively inverted such that time becomes space and space becomes time. A temporal volume where all paths of causality lead down towards the singularity and where all of past history begins at the enclosing event horizon; the black hole.
However this for me is not a conclusion that is purely mathematical but one drawn from the realm that lies beyond the veil. Specifically, death or rather listening to those who have had near death experiences themselves.
As always, the internal conflict between the strict logical rational materialist and the rest of my humanity kicks in. But as witness testimony in a murder case is enough to convict a man for life so too am I comfortable with listening to those whose testimony I believe. And if such an experience can change the entire belief structure of a man like myself, a scientist, then such a level of evidence is good enough for me.
That and I just need to remind myself of the muse that drives this work now.
Eben Alexander’s talk to the Theosophical Society recounting his near-death experience. What makes Eben’s account so interesting is that because of the type of meningitis that he had it effectively nullifies the idea that such experiences arise from the release of neurotransmitters like DMT. [15] [16]
Specifically it was this description by Eben Alexander, an MIT neurologist, who experienced a near death experience when he was suddenly stuck down by meningitis. Just listen to his explanation and his description while thinking about a place of one spatial dimension enclosed inside a temporal volume; the ecosystem of souls dreaming of their lives past and yet to be. All paths leading unto Him/Her/Insert your name of God here; the naked singularity. [15]
In particular it is in his description of learning how to move through this realm. By remembering the tune, the melody, the song he managed to travel from his “earthworm view” up through the valley and back into “the core”. One unidirectional spatial dimension whose melody is the song of the cosmos. Or listen to his description about how he followed the light as he circle his finger upwards in a CPT-Symmetric fashion; “that spinning melody that came towards me”.
To quote, “Time flow in that gateway realm is very different from time flow here.” as he describes how we experience all of our life in a single moment learning all the lessons of life. “Time flow and causality are of a much higher order in that realm.”
In describing “the core”, to quote (video timestamp 54:59), “and what I remember is all of that collapsing down. The material world is four dimensional spacetime collapsing down and the deeper time of causality in that beautiful gateway valley where we often are between lives. Until I emerged into a realm that I call the core.” as being a place full of souls all planning their next life. I’ll stop short of trying to describe what a naked type-V being looks like. Sounds to me that its energy source is a white hole sitting in the exact position where all lines of causality meet.
Off course it does make me reflect on three aspects of my life. Firstly, is the slight inconvenient truth that I started down this path of studying medicine and physics in my teenage years driven by an internal story narrative in planning my next reincarnation. That internal story narrative now has become the anvil upon which the Big Bang Hypernova Hypothesis has been forged. Secondly, in order to understand one dimensional spatial reality in all its mathematical detail a person would have to become a world class expert in information theory, compression and audio. Lucky for me, seeing as I would happily describe myself as a walking encyclopaedia in audio compression technology. Thirdly, have you seen the artistic inspiration for my logo?
Off course, get me drunk enough and I’ll probably personally introduce you to several pantheons and their personal politics. Though I wouldn’t be too surprised if the pub suddenly burnt down because it was hit by lightning just at the very moment I’m about to open my stupid Gob.
Returning to the realm of “how do I define this recursive idea in mathematical terms” I am drawn towards that discovery which is already known by alien intelligence. All I have to do is describe it using the existing notation set forth by my fellow peers; the accumulated wisdom of the ages.
A central pillar that I use as a basis for my hypothesis are the set of Penrose-Hawking Singularity Theorems. A consequence of those theorems being this description in how space-time inverts itself into becoming time-space. However in order to explore these theorems let us start at the beginning with Einstein’s Field Equations of General Relativity.
$$ G_{\mu\nu}+\Lambda g_{\mu\nu} = \frac{8 \pi G}{c^4} T_{\mu\nu} \phantom{xxxxxxxxx}(1) $$
In a nutshell it describes the relationship between the curvature of spacetime and mass. More specifically, \(G_{\mu\nu}\) is the Einstein, or trace-reverse Ricci, tensor which is used to describe the curvature of a pseudo-Riemann manifold. On the other side, \(T_{\mu\nu}\) is the stress-energy tensor which represents the distribution of energy, momentum and stress in the spacetime manifold. Here \(G\) is the universal gravitational constant and \(c\) is the speed of light.
The \(\Lambda\) is called the cosmological constant and \(g_{\mu\nu}\) is the metric tensor which Einstein introduced in light of the predominate cosmological model at the time, the steady state model. The consequences of it not being in his equations, as Lemaître showed, was that the universe had to have been born in the Big Bang. Calling it his greatest blunder Einstein subsequently removed the term after Hubble demonstrated to Einstein that our universe is indeed expanding. [17] [18]
However, since the unexpected discovery of dark matter and then subsequently dark energy it has since come back into fashion. In effect, the term is a source term that tries to fix the problem of why we not only see an expanding universe but one whose expansion is actually accelerating. It is Lambda of the \(\Lambda\)-CDM model which manages to nearly to annihilate itself in the first \(10^{-50}\) seconds according to its explanation. With respect to the Big Bang Hypernova Hypothesis, as we’ll see and have discussed, proposes an alternative solution to this source term; namely a White Hole. [19]
The Einstein field equation shown in (1) is a compact 4-by-4 notation that when unpacked produces a series of partial differential equations. Solutions to these equations yields a description of spacetime, a Lorentz manifold. Like solving most partial differential equations a number of assumptions and constraints are first made in order to solve them such that we arrive at a given solution or metric.
One such solution, the first and the simplest, is the Schwarzschild solution or Schwarzschild metric. This exact solution is named after Karl Schwarzschild who in 1915 formulated it in the months proceeding Einstein’s publication showing his equations of General Relativity. [20]
The Schwarzschild metric, shown in (2), describes the gravitational field outside a spherical mass based on the assumption that both the electric charge and angular momentum of the mass, as well as the cosmological constant, are all zero. In effect, the solution is a useful approximation for describing slowly rotating astronomical objects such as planets and stars. [21]
$$ ds^2=-c^2 d\tau^2 = -(1-\frac{r_s}{r})c^2dt^2 +\frac{dr^2}{1-\frac{r_s}{r}} +r^2(d\theta^2 + sin^2\theta d\varphi^2) \phantom{xxxxxxxxx}(2) $$
Expressed in spherical coordinates a point in space is represented as \((r,\theta,\varphi)\). The centre of the spherical astronomical body is at \(r=0\). Here \(\tau\) is the time measured by a clock moving with the particle in seconds; \(t\) is the coordinate time as measured by a clock at infinity or rather in a perfectly flat spacetime geometry. The Schwarzschild radius, denoted by \(r_s\), relates the mass of the body \(M\) via the equation shown by (3) where \(G\) is the universal gravitational constant.
$$ r_s=\frac{2GM}{c^2} \phantom{xxxxxxxxx}(3) $$
Before we can begin to talk about the Schwarzschild metric we need to understand the various spacetime diagrams developed in order to simplify and communicate the theories of relativity and their associated solutions. [22]
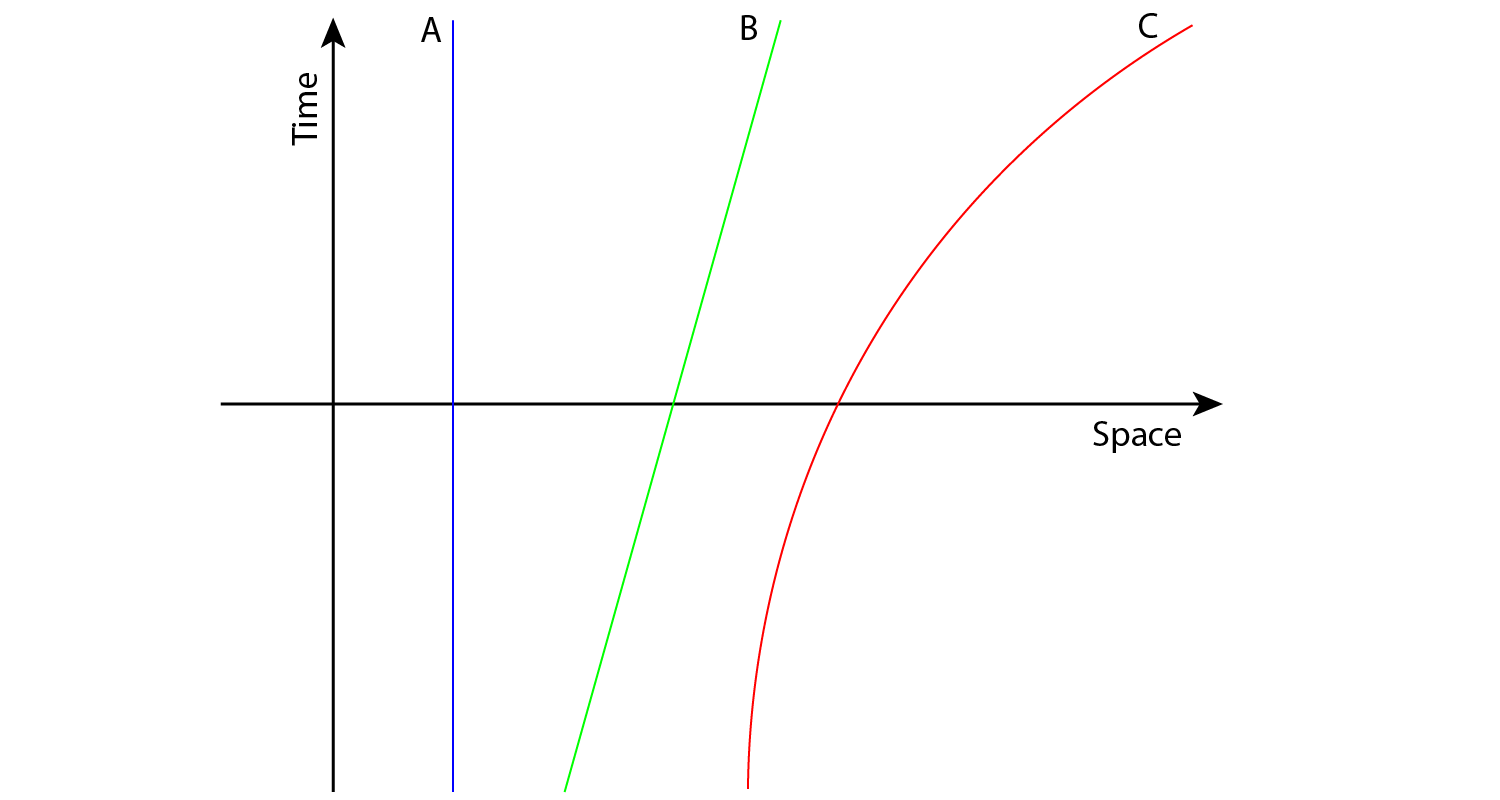
Graph showing time plotted on the vertical axis and space, which also equates to distance, on the horizontal axis. This is the simplest spacetime diagram. (A) The blue line plots the world line of a stationary object. (B) The green line plots the world line of an object with constant velocity. (C) The red line plots the world line of an object under-going acceleration. The closer the world line’s gradient is to running parallel with the horizontal the faster the object is moving.
The first and simplest spacetime diagram is a 2-dimensional graph plotting time on the vertical axis and space on the horizontal axis. Used in classical non-relativistic Newtonian physics this graph plots the path travelled by an object over a period of time. So on the horizontal axis, x-axis, we plot the dimension of length to represent spatial distance and on the vertical axis, y-axis, we plot the dimension of time to represent the unidirectional passage of time. The line upwards points to the future and downwards points to the past.
An object at rest, with no spatial movement, would plot a vertical line on the graph. An object at constant velocity, hence constant gradient, would plot a straight line on the graph. The plotted path of an object we call its “world line”. We can see the faster an object travels the smaller the gradient of the world line; coming closer and closer to being parallel to the horizontal. Thus an object travelling with infinite velocity would have a flat world line on the graph running parallel to the x-axis. An object moving at the speed of light would produce a nearly horizontal line.
Hermann Minkowski, Einstein’s former professor in 1907, developed the first relativistic spacetime diagram in order to give the Special Theory of Relativity a geometric representation.
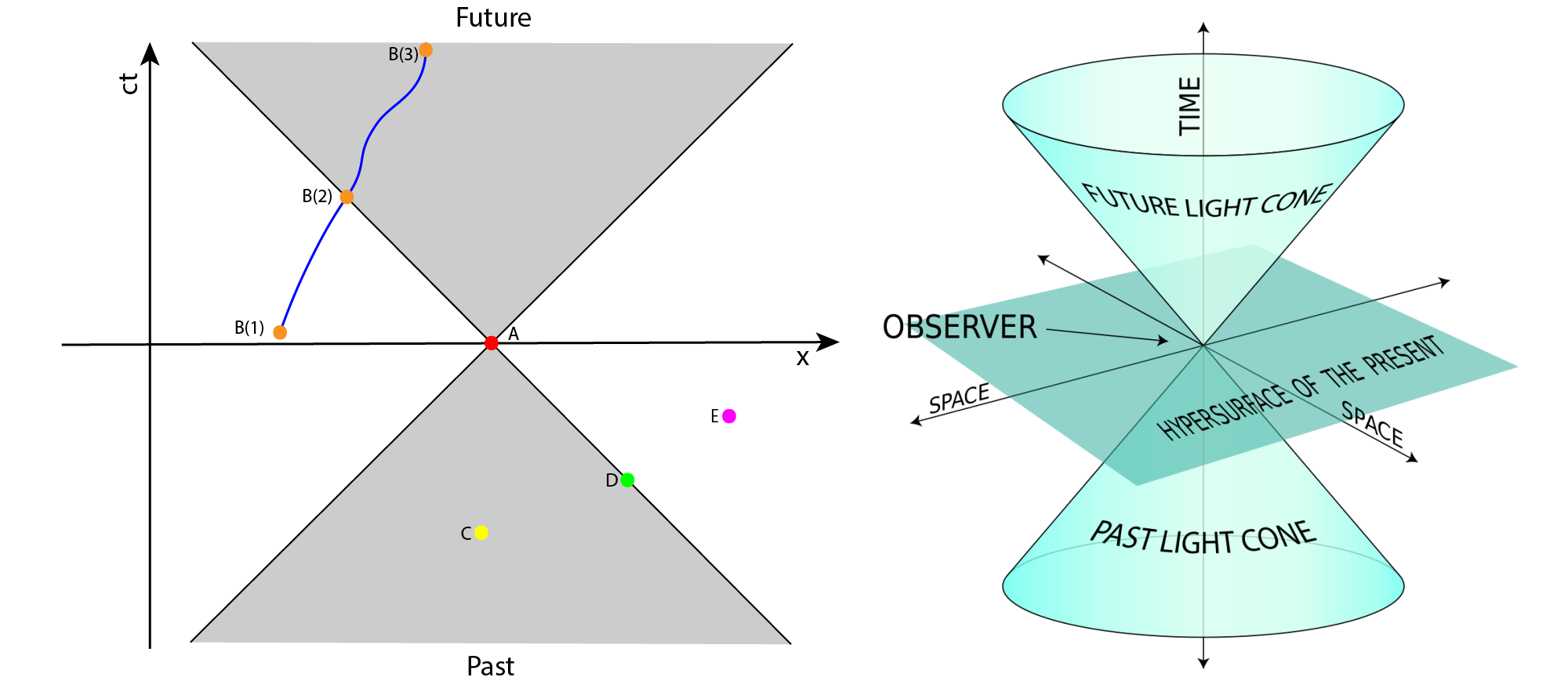
In a Minkowski spacetime diagrams photons, travelling at the speed of light, have a gradient which is at \(45^\circ\) to the horizontal. Drawn from a point of interest, marked in red at A on the left, the light cone determines the observable horizon both into the past and future for the given location in spacetime. The left hand diagram depicts a single spatial dimension on the horizontal and time on the vertical. The right hand diagram depicts a 2-dimensional space upon the horizontal plane and time on the vertical.
Looking back into the past, an observer at point A will have knowledge of event C, sitting inside the light cone, implying that A has witnessed event C. The observer at A will see the light coming from event D as it sits on the surface of the light cone. The observer at A will have no knowledge of event E, sitting outside the light cone, as not enough time has past for photons from E to have reached the observer at A.
Looking into the future, from the moment an event happens at A we follow the world line of observer B. B at position 1 has no knowledge of A as light from the event has not reached the observer. The observer witnesses and hence can know about event A when it is at position 2 where the world line intersects with the light cone of event A. Inside the light cone B now has knowledge of event A.
In a Minkowski diagram the coordinate system is chosen such that a photon, travelling at the speed of light, would produce a line with a gradient of \(\pm 1\). i.e. At \(45^\circ\) to the horizontal. The history of an object’s location throughout all time traces out a line, referred to as the object’s world line, in a spacetime diagram. Points in a spacetime diagram represent fixed positions in both space and time and are referred to as events. Here the word “event” is used as abstraction to some kind of event like a hypernova explosion or a particle reaction which emits photons. It is this configuration, where photons travel at \(45^\circ\) to the horizontal that is key to understanding how to interpret a relativistic spacetime diagram.
Plotting two lines at \(45^\circ\) produces a triangle, or a light cone in 3D, spanning upwards from the fixed location and time of a given event. An observer inside the volume of the light cone will be able to have knowledge of the event because it has been able to see the event. The point at which an observer sees an event is the point in the observer’s world line where it intersects with the surface of the given light cone. Any observer outside of this light cone will have no knowledge of the event as not enough time has passed for the light from the event to have reached the given observer.
In inverse, a light cone can span downwards, into the past from a given fixed position in space and time. The volume of the downward light cone represents the observable horizon for the given fixed position. Any event happening outside of this past light cone will mean the observer will have no knowledge off it because light travelling from the event has not reached the given fixed position. Vice versa, an observer can have knowledge of an event happening if it falls inside the volume its past light cone. This is because light from the given event has previously managed to reach the position in space where the line cone is fixed at. What light an observer sees at a given fixed position in both time and space lies upon the surface of the downward cone.
Special Relativity tells us that if an object has mass then it can never travel at or faster than the speed of light. Thus when plotting the world line of an object that has mass upon a Minkowski diagram its gradient must always be greater than \(45^\circ\) to the horizontal. If it was then this would be a violation against the law of Special Relativity.
Penrose diagrams, or Carter-Penrose diagrams, are a variation to the Minkowski diagram. Named after Brandon Carter and Roger Penrose who were the first to use them these conformal diagrams employ a coordinate transformation that captures an infinite expanse of both space and time into a finite diagram. In order to understand why we need a coordinate transformation we first need to talk about singularities.
A singularity in mathematics is a point at which a given mathematical object ceases to be well-behaved in some particular way. For example the real-value function (4)
$$ f(x)=\frac1x \phantom{xxxxxxxxx}(4) $$
has a singularity at \(x=0\) where it seems to explode to \(\pm\infty\). The Schwarzschild metric has two mathematical singularities at two locations; where \(r=r_s\) and \(r=0\).
At first, these singularities were not really considered a problem because the metric solution was intended to model the gravitational field of large astronomical bodies such as our Sun. Here the Schwarzschild radius is far smaller than the radius \(R\) of a given body; i.e. \(r_s<R\). For example the radius of our Sun is 700,000km while its Schwarzschild radius is only 3km. As we cannot see inside a given body, such as the Sun, then we cannot know or measure anything about it. Hence why it was seen at first as not being of any great relevance.
However over the coarse of the first half of the 20th century physicists discovered and developed the new science of quantum mechanics. In particular, astrophysicists came to understand the role of nuclear fusion and the subsequent life cycle of stars. It was in considering novae and core-collapse that serious questions began to be asked in regards to the exact nature of these mathematical singularities within the Schwarzschild metric.

The singularity at \(r=r_s\) divides the solution into two disconnected regions. The exterior solution for all \(r>r_s\) is coloured blue. The interior region, coloured red, where \(0\leq r <r_s\). At the centre of the interior region is the singularity at \(r=0\).
The mathematical singularity at \(r=r_s\) divides the whole into two disconnected regions. The exterior Schwarzschild solution is covered by the region for all \(r>r_s\) and it is this solution that is used to model gravitational fields of stars and planets. The interior Schwarzschild solution where \(0\leq r <r_s\), which contains the singularity at \(r=0\), is completely separated from the outer region by the singularity at \(r=r_s\).
The singularity at \(r=r_s\) is called a coordinate singularity. That is, the discontinuity seen at \(r=r_s\) can be resolved by using a different coordinate system for the Schwarzschild solution. Over the years a number of coordinate systems have been developed. For example there is Lemaître coordinates, Eddington-Finkelstein coordinates, Kruskal-Szekeres coordinates, Novikov coordinates and Gullstrand–Painlevé coordinates. However, as noted, we’ll specifically discuss a conformal coordinate transformation that renders us Penrose diagrams.
By changing to a different coordinate system the metric then becomes regular at \(r=r_s\) such that the external region can now be extended to values of \(r\) smaller than \(r_s\). Thus, in using a different coordinate system we able to extend the external region into interior region. It is this extension of the manifold solution, by using a different coordinate system, that gives the prefix to a spacetime diagram’s description. For instance when applied to the Schwarzschild diagram we say the diagram shows an “extended Schwarzschild solution”.
For a Penrose diagram, we define a static infinite Minkowski universe where every point can be described by the real-valued coordinate pair \((x,t)\). So imagine an infinitely big piece of a graph paper that is itself a Minkowski diagram. We transform every point upon the infinite Minkowski diagram into a finite 2-dimensional area, which is described by the coordinate pair \((u,v)\), using the transform given by equation (5).
$$ tan(u \pm v)=x \pm t \phantom{xxxxxxxxx}(5) $$
Doing so renders us the basic unit of a Penrose diagram. Like a Minkowski diagram space is orientated on the horizontal and time on the vertical. Also the path of any photon or light ray follows a line with an angle of \(45^\circ\), just like a Minkowski diagram.
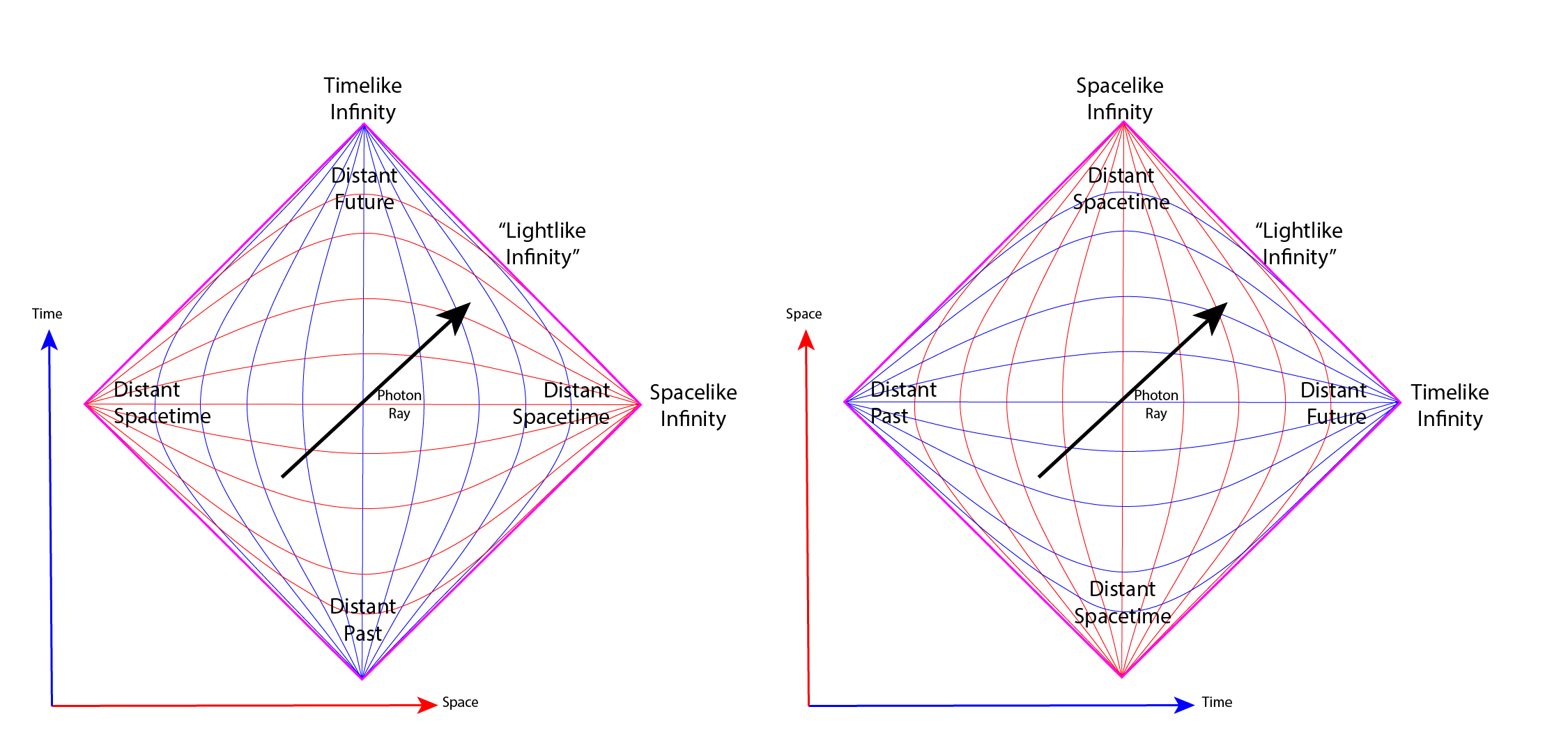
The units of a Penrose Diagram encapsulate entire spacetime solutions inside a finite conformal, local angle preserving, diagram. The conformal nature of the diagram allows light “photon” rays to be drawn at \(\pm45^\circ\) degrees. The left hand unit shows a space-geodesic universe such as an infinite Minkowski universe. The right hand unit shows a time-geodesic universe such as the one found inside the event horizon of a Schwarzschild black hole. Red lines are spatial dimensions and blue lines are temporal dimensions. Notice how the dimensions swap roles between being a space-geodesic and a time-geodesic.
The biggest difference is that locally, the metric on a Penrose diagram is conformally equivalent to the actual metric in spacetime. The transformation (5) is a conformal mapping which means that locally it preserves the angle. In mathematics, conformal geometry is the study of the set of angle-preserving, known as conformal, transformations on a space. So the reason the photon preserves its angle of \(\pm45^\circ\), in its coordinate transformation from a Minkowski diagram, is because (5) is a conformal mapping which locally preserves the angle.
Fixing the temporal coordinate, \(v=0\), note that as \(u\rightarrow\pi/2\) so by the tangent function in (5) does it imply that \(x\rightarrow\infty\) giving us our “Space-like Infinity” in the right-hand corner. Vice versa, as \(u\rightarrow -\pi/2\) then \(x\rightarrow-\infty\) giving us our “Space-like Infinity” in the left-hand corner.
Repeating this process but rather this time we fix the spatial coordinate, \(u=0\), then note that as \(v\rightarrow\pi/2\) so by the tangent function in (5) does it imply that \(t\rightarrow\infty\) in the infinite future; giving us our future “Time-like Infinity” in the top corner. Vice versa, as \(v\rightarrow -\pi/2\) then \(t\rightarrow-\infty\) in the infinite past; giving us our past “Time-like Infinity” in the bottom corner.
Hence we can see how an infinite Minkowski universe can be mapped into a finite diagram.
Another very important property in this choice of conformal mapping is that every point on a Penrose diagram can also map to a 2-dimensional point upon a sphere \((\theta,\phi)\). This means that it can also be used to represent spherically symmetric spacetimes such as that contained within the spherical event horizon of a Schwarzschild black hole.
With this all said we can return to discussing the singularity at \(r=0\) within the Schwarzschild metric. In the context of theoretical physics in the 1950s and 60s the question, “What happens at the core of a star going nova?” was key. Could a massive star collapse so completely upon itself as to become both infinitely dense and curved as told to us by the Schwarzschild metric?
It was Roger Penrose who applied a rigorous mathematical analysis to this question which culminated in his 1965 Singularity Theorems. Specifically it was his letter “Gravitational Collapse and Space-Time Singularities” to the Physical Review Letters that earned him the 2020 Nobel Prize. [9] [23] [24]
Off course Penrose’s 1965 singularity theorem specifically focuses on that subject which is the very centre piece of my hypothesis, namely a hypernova. Now in my essay describing exactly what a hypernova is we saw the reason for why core-collapse happens; the fusion of iron. I describe that the event of core-collapse into a black hole as a matter fact. But it was through this theorem that Penrose showed that the existence of black holes was a logical consequence of Einstein’s Theory of General Relativity.
A bit of context is important in remembering that neutron star’s were first theorised by Fritz Zwicky in 1934. But it wasn’t until 1967 when Jocelyn Bell first observed neutron star’s as pulsars that physical confirmation of their existence was confirmed. Kind of like proposing the idea that there exists a starlike object in a place called the Superverse whose diameter is measured in the hundreds of millions light years. I had a great deal of trouble trying to imagine it myself until the Boötes Void gave it shape. [25] [26]
I remember growing up hearing the ongoing debate about black holes and their existence. Much of that debate centred on Cygnus-X1 one of the brightest X-ray sources in the sky. Quasars were unbelievably bright objects at the edge of the universe. Since then we have learned about how a supermassive black hole resides at the centre of nearly every galaxy. We have directly observed the gravitational effect of the Milky Way’s own supermassive black hole, Sagittarius A*. Now, with the development of the Event Horizon Telescope, we have been able to directly observe the black hole at the centre of the M87 active galaxy by following its jet back to the source. [27] [28]
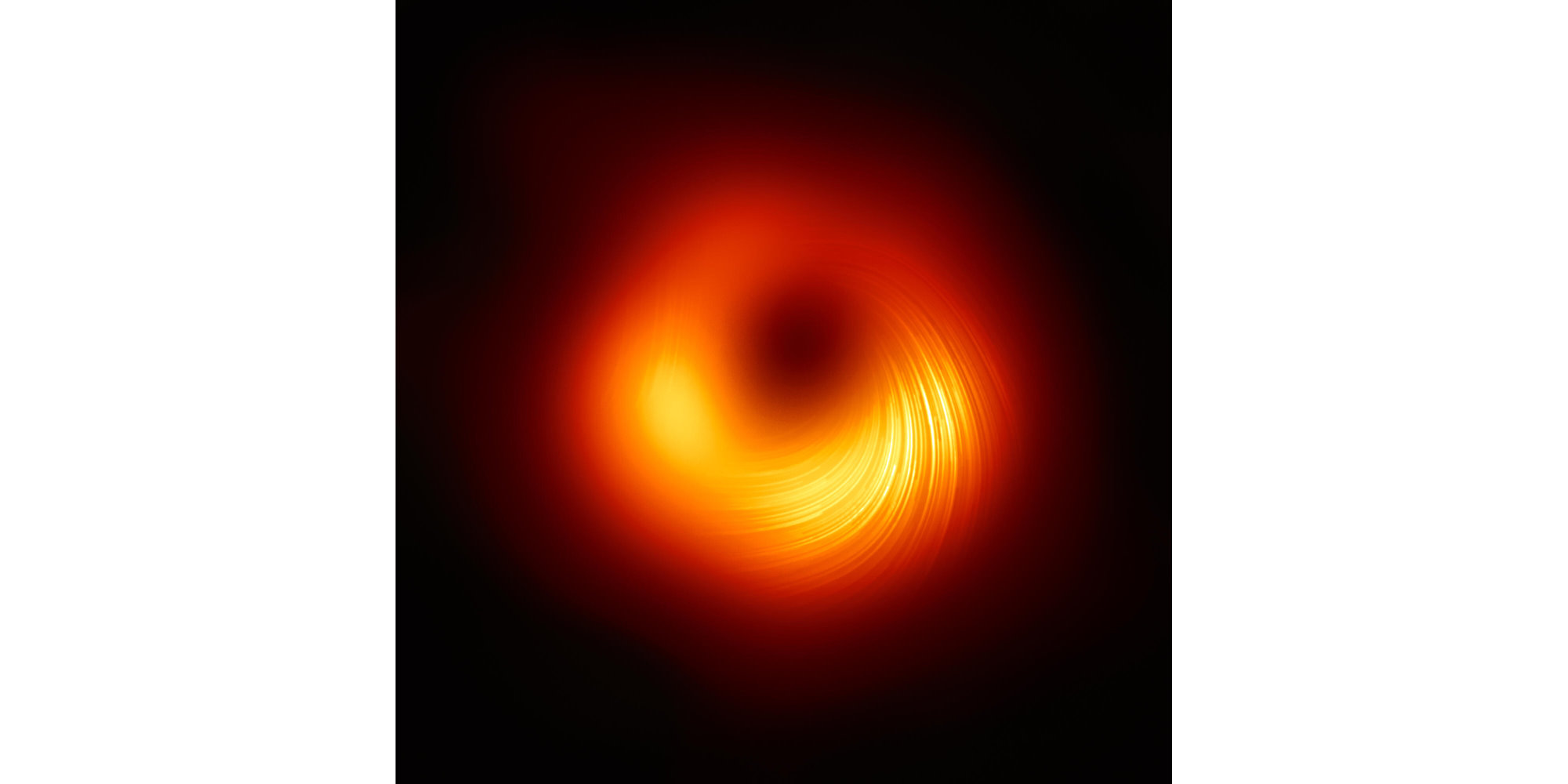
A view of the M87 supermassive black hole in polarised light: The Event Horizon Telescope (EHT) collaboration, who produced the first ever image of a black hole released in 2019, has today a new view of the massive object at the centre of the Messier 87 (M87) galaxy: how it looks in polarised light. This is the first time astronomers have been able to measure polarisation, a signature of magnetic fields, this close to the edge of a black hole. This image shows the polarised view of the black hole in M87. The lines mark the orientation of polarisation, which is related to the magnetic field around the shadow of the black hole. Credit: EHT Collaboration [28]
It was this direct observation of a black hole that saw Roger Penrose win the Nobel Prize in Physics. Such was the importance of Penrose’s 1965 singularity theorem.
What the theorem does is to show how the curvature of spacetime becomes entrapped in the core-collapse of a massive star. So driven by both the absorption of energy coming from the fusion of heavier elements and the weight of the star down upon itself the process of core-collapse begins. An initial curvature exists, down towards the centre, coming from the mass of the star. As the core-collapses down in on itself the density of matter at the core continuously increases. This increase in the density of matter further increases the curvature of spacetime.
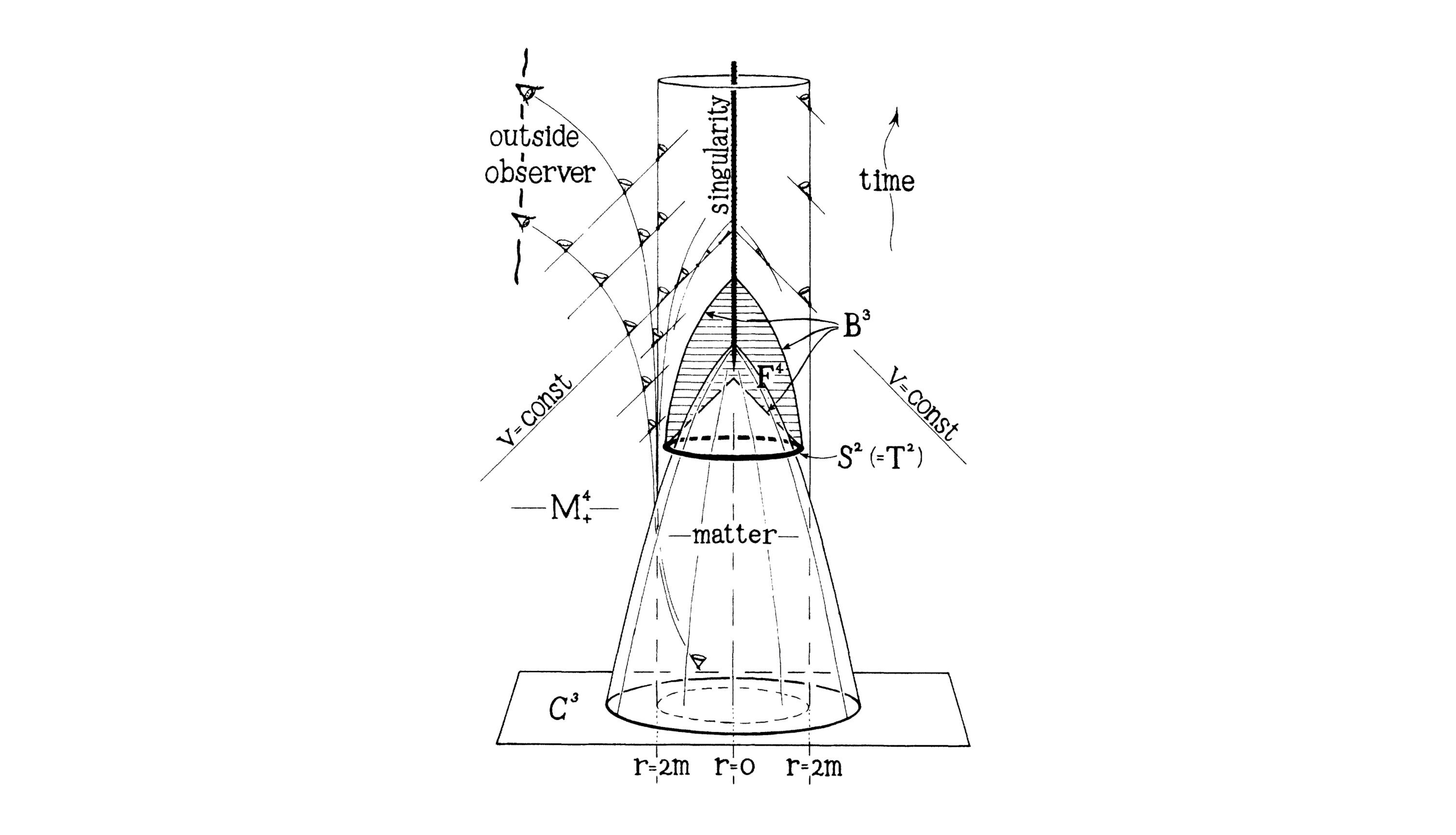
Penrose’s illustration, from his original publication, showing the symmetrical core-collapse of matter within the Schwarzschild radius. It shows how the increased curvature within the collapsing core causes the light cones to become entrapped within the Schwarzschild radius such that all paths of probable casualty collapse onto a single point singularity. [23]
At some point the curvature of spacetime becomes so great that all future lines of causality, as depicted by the light cones, become entrapped. In the symmetric case, the Schwarzschild metric, the surface of an event horizon is born at the Schwarzschild radius. Inside this radius all the future light cones are enclosed inside the spherical volume that we now call the event horizon. Not only this but all the future light cones point and finally converge upon the singularity at the centre. Penrose also then considers the asymmetric case in employing the newly formulated Kerr metric and found that it to also collapses down to a physical singularity.
Using a Penrose diagram we draw the whole solution for the Schwarzschild metric. [22]
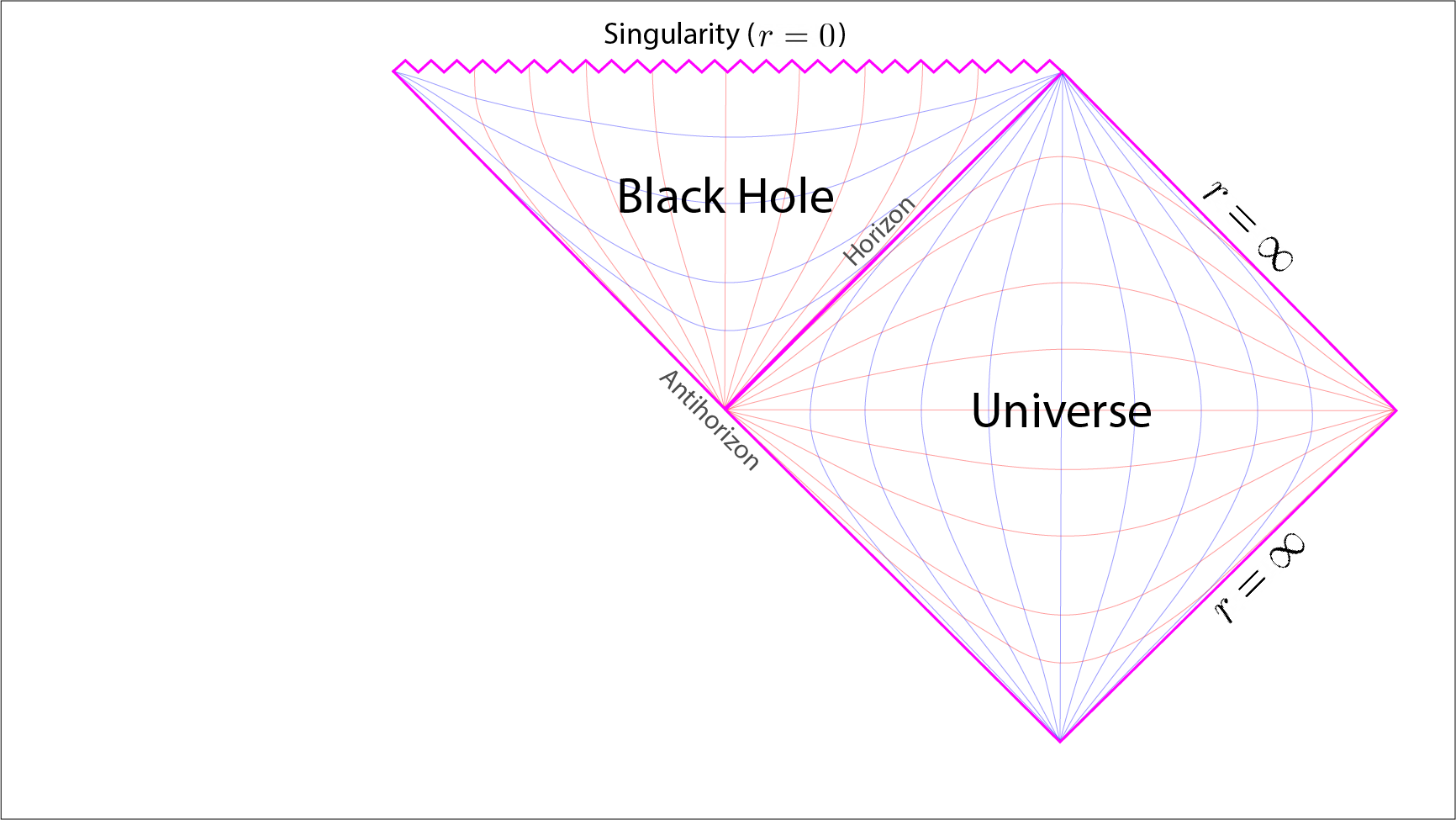
Penrose diagram of a Schwarzschild black hole. [2]
The right-hand diamond represents the infinite Minkowski universe outside the black hole. The triangle to the upper left represents the spherical spacetime solution inside the black hole. The two distinct regions are connected at the Schwarzschild radius where the event horizon of the black hole is located. The point singularity, at \(r=0\), is represented by the jagged line running along the top of the black hole’s triangle.
The blue lines inside the triangle represent the dimension of time. The red lines inside the triangle represent the dimension of space within a given universe. Here a given universe is the spacetime solution entrapped inside a given diamond or triangle. So in this diagram we have two entrapped solutions of spacetime; the Minkowski universe on the right and the black hole in the upper triangle.
A very important feature of a Penrose diagram, as we discussed early on, is that the roles a given dimension plays is effectively inverted. That is a spatial dimension becomes a temporal dimension. Vice versa, the unidirectional dimension of time becomes a unidirectional dimension of space. It is unidirectional as the only causal path of travel is down towards the singularity at the centre. This interpretation is reflected in a Penrose diagram by the spatial lines being coloured as temporal lines. And vice versa, temporal coloured lines become spatially coloured lines once inside the event horizon. So note how the dimensions of time and space are interchanged inside the black hole in comparison to the Minkowski universe given inside the right-hand diamond. This captures the interchange in the role a dimension plays within a given universe.
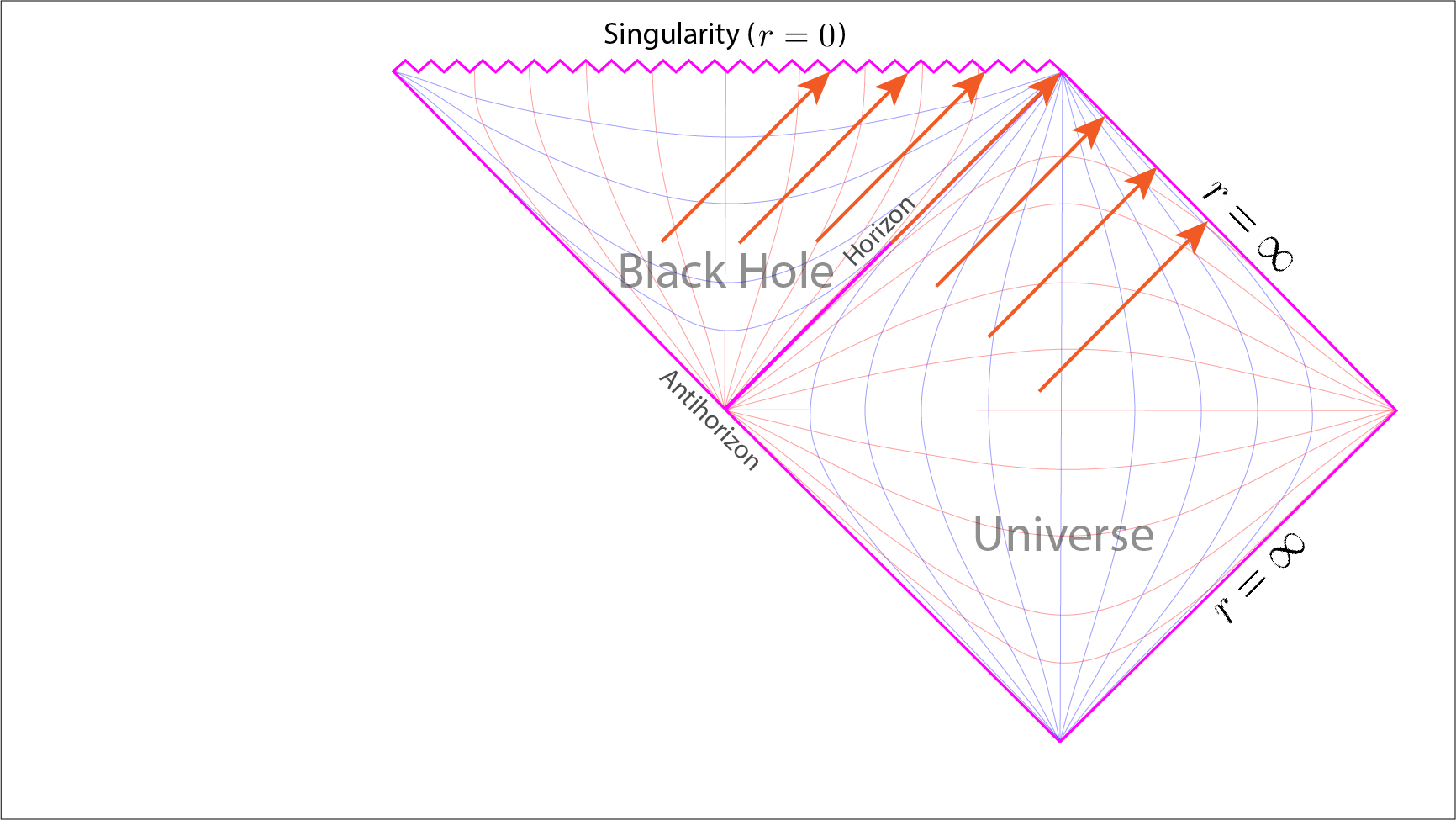
From the Penrose diagram light rays originating inside the universe are seen travelling forever towards the light-like infinite future. On the other hand, light rays originating inside the black hole are seen to be collapsing onto the singularity. The light ray on the event horizon itself extends infinitely into the future following the curvature of the event horizon.
Note that the line of the event horizon is at \(45^\circ\) and extends infinitely into the future. A photon whose direction of travel is tangent to the event horizon will always follow the curvature of the event horizon. Thus the photon is infinitely trapped upon the event horizon and this is what is represented by the event horizon line on a Penrose diagram.
If we draw a series of light ray lines, each at \(45^\circ\) clockwise and thus running parallel to the event horizon, then we see a light ray can meet with one of two fates. If the line is inside the black hole region then its future is to collapse onto the singularity. Outside of the black hole the line travels of into the infinite space and future.
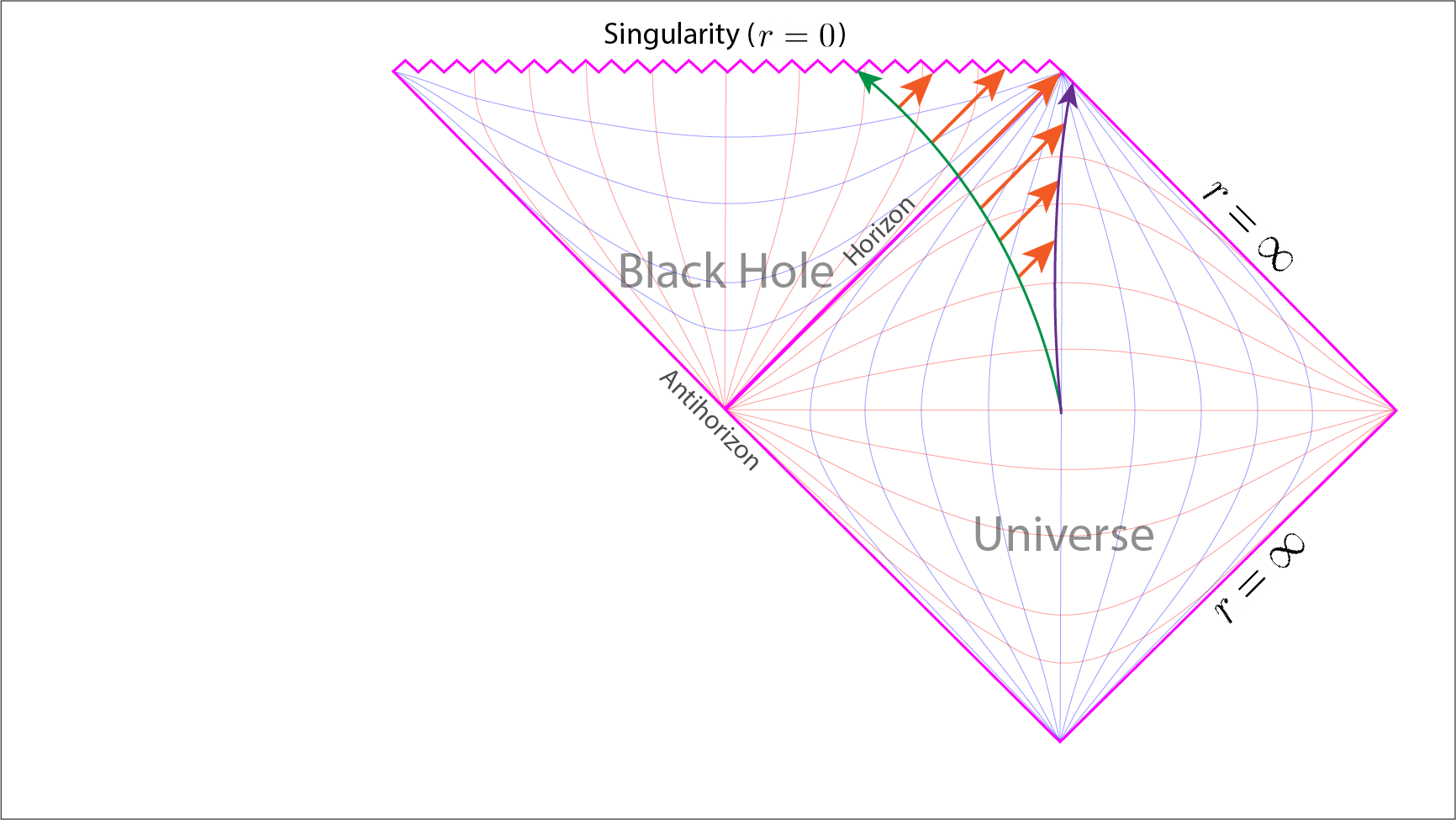
Penrose diagram showing two objects with mass. One object, following the green path, falls inside the black hole to meet its end upon the singularity. The other object acts as a fairly stationary observer, following the purple path, out to the time-like infinite future. The length a light ray, coming from the in-falling object, has to travel becomes greater and greater, until it becomes infinite, the closer the object is to the event horizon. At the horizon the light ray is actually trapped upon the horizon. Once the object has fallen beyond the horizon the light ray is trapped inside the event horizon with its path ending upon the singularity.
Now let us consider an object, with mass, falling into a black hole. We plot the object’s world line as it falls through the event horizon from the infinite Minkowski universe into the black hole. Once inside the event horizon its eventual fate is to fall unto the point singularity at \(r=0\).
We now plot the light rays, at \(45^\circ\) clockwise, moving from the object towards the observer. Thus the closer to the event horizon the longer the light ray. Remembering that the closer to the top corner we get the greater the expanse of time, until it is infinite. This in turn implies light takes longer and longer to reach the observer the closer the object gets to the event horizon. In effect the light from the object that the observer sees will be increasingly redshifted the closer it is to the event horizon.
But ultimately, the observer will never see them fall through the event horizon. At the event horizon the light ray is trapped on the event horizon itself. Past the event horizon a light ray is now destined to fall onto the singularity.
On the other hand, the object will see itself fall through the event horizon in a finite amount of time. Any light emitted by the object, once across the event horizon, will now be destined to hit the singularity. This we can see illustrated on the diagram by the \(45^\circ\) light ray lines. The final fate of the object, like the aforementioned light rays, is to collapse onto the singularity.
With all this said, we have now plotted out the complete Schwarzschild solution which covers both our universe and a non-rotating black hole in the context of a Penrose diagram. However this is only half the picture as we can extend the solution even further. The solution discussed so far covers the unidirectional arrow of time going forward from the past into the future. We can extend the solution by considering the idea of time-reversal.
The mathematical trick comes from defining the metric such that it has I guess a finite beginning. As opposed to having an infinite past. Hence we can view the Penrose diagram as starting from the time of the Big Bang. Here so far we have only considered the solution for \(X>T\), meaning travelling forwards in time from the moment of the Big Bang. But we can extend the solution for \(X<-T\), travelling backwards in time away from the Big Bang, which is the time-reversal solution. [29]
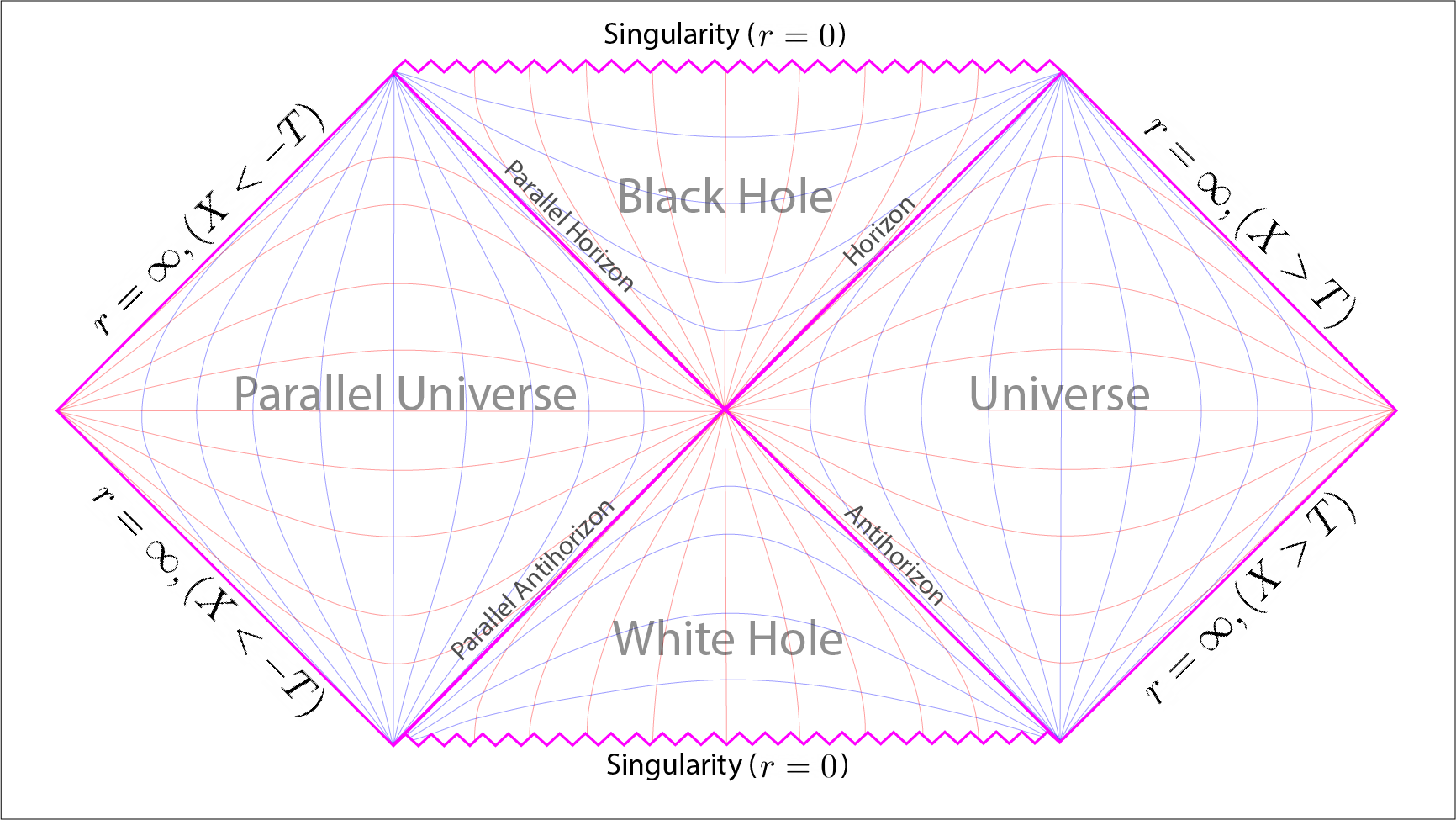
Penrose diagram showing the extended Schwarzschild solution which has been extended by considering a reversed arrow of time from the moment of the Big Bang. Where the arrow of time is directed forward, \(X>T\), then we have our universe and the black hole. Where the arrow of time is reversed backwards, \(X<-T\), then we have a parallel time-reversed universe and a time-reversed black hole; better known as a white hole.
Applying this extension to our Penrose diagram renders the extended solution. The new diamond on the left is in effect a new parallel universe that is the opposite our own universe, situated upon the right. The key difference is that the arrow of time runs in the opposite direction to our own universe. In totality this new parallel universe is a direct consequence of considering time-reversal in the context of General Relativity.
In my “CPT-Symmetry inside the Superverse” work I explicitly show how the pattern of a hypernova can give rise to two a pair of CPT-Symmetric jets. Moreover we looked at the work of Andrei Sakharov and his 2D-didactic cosmological model in considering both baryon asymmetry and CPT-symmetry. This too considered a time-reversal parallel universe composed of anti-matter on the opposite side of the Big Bang. In this work, I explicitly argued that the reason why matter and anti-matter are what they are is a direct consequence following the pattern of a hypernova. That is, the solenoid magnet field shapes the jet itself and hence the CPT-Symmetric pattern. However this is a result in the context of Quantum Mechanics. [30]
The Big Bang Hypernova Hypothesis explicitly sees the creation of our universe as being one of the output two jets. It sees the other jet as being our twin universe whose directional arrow of time is opposite to our own. So from the point of view of my hypothesis this extension is not just a mathematical trick. Both Quantum Mechanics and General Relativity are saying the same thing that there exists a time-reversed parallel universe to our own.
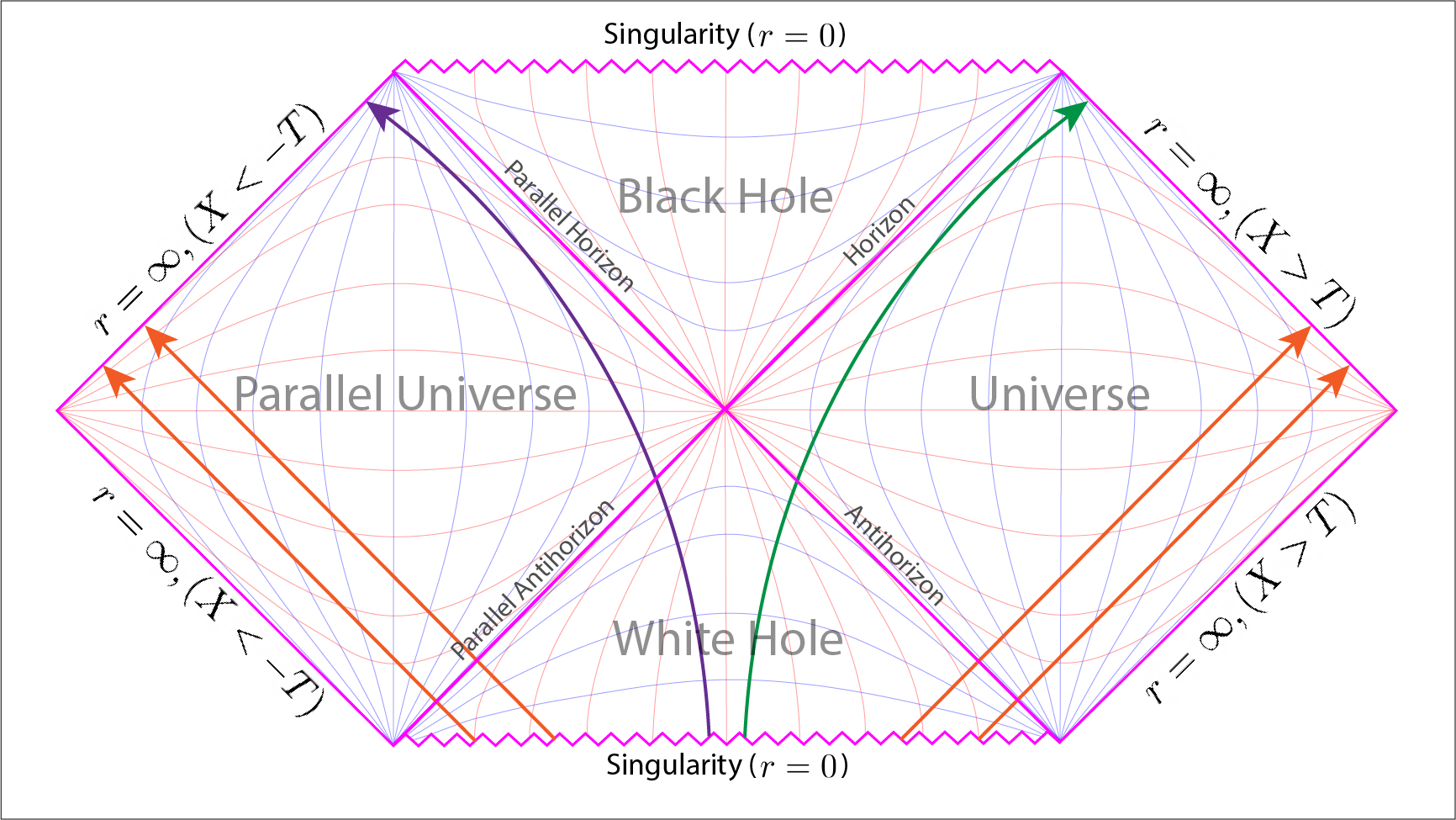
Light rays, orange lines, start their journey from the White Hole’s singularity travelling out into either our universe or the parallel universe. The green path shows an object’s world line from the centre of the white hole out into the infinite future of our universe. The purple path shows an object’s world line from the centre of the white hole out into the infinite future of the time-reversed parallel universe.
The connection between them comes in considering a time-reversed black hole or what has popularly become known as, namely, a White Hole. In the Penrose diagram of the extended Schwarzschild solution the white hole is the triangle at the bottom. Here an object travels away from the point singularity, at the base of the triangle, out towards the event horizon where it is ejected. In complete opposite to a black hole the unidirectional spatial dimension is away from the singularity and up towards either one of the two event horizons. Thus a particle will either emerge out into either our own universe or our time-reversed parallel universe.
Nothing can cross the event horizon of a white hole from the outside into its interior. This is in inverse to a black hole where nothing can escape back out of the event horizon once across it. Light-rays, as we can see on the Penrose diagram travel out from a white hole but can never fall into it. So in totality a white hole is a time-reversed black hole.
More importantly, in the context of the Big Bang Hypernova Hypothesis it finally gives me a causal mechanism in giving it a very specific reason as to answer the question: How and why did our universe come into existence?
Ever since the 1960s, when white holes were theoretically proposed, many cosmologists have seen this is as a causal mechanism for the Big Bang. A critical component in the actual Big Bang theory is some kind of gravitational singularity. If we could watch time being rewound to the moment of the Big Bang we would see the entire universe shrink and condense back down onto this gravitational singularity. [31]
The reason for saying that the Big Bang requires a gravitational singularity comes from Steven Hawking’s work after Roger Penrose showed him his singularity theorem. Hawking, for his Phd thesis, applied Penrose’s singularity theorem in the context of a cosmological model. Applying it to the Big Bang itself he found that a singularity was inevitable. Hence the reason for my assumption that the Big Bang requires some kind of gravitational singularity and what is born inside a hypernova event; by Penrose’s singularity theorem. [32] [23]
Although cosmic inflation is the current flavour of the institutes the use of white holes as an explanation for the Big Bang is a popular alternative. This paper tries to revive the idea of white holes in cosmology with the idea that small bangs inside our universe create gamma-ray bursts. Like it, close, but one thought is “causally and continuously closed vacuum space” entangled with a Gamma-Ray Burst; the Jet-a-verse. [33]
Or there is this paper using a 5D solution which I think is the same framework used in the film Interstellar and its depiction of the “bulk”. Another physics letter by Nikodem J. Poplawski which sees a universe being born inside a black hole. This is almost the closest, in my humble opinion, but fails to see the larger Superverse or my lovely Fermi Bubbles. The pathway to the new universe is inside the black hole but both verses share the same spatial dimensions and locations. [34] [35] [36] [37]
To understand this point of view, in the context of the Big Bang Hypernova Hypothesis, we need to see the casual connection between the Superverse and our universe. In order to see this we need to start by adding one of my hypothesis’s key ingredients, namely rotation.
As mentioned, the Schwarzschild metric is the simplest solution to Einstein’s Field Equations. This solution makes the assumption that both the electric charge and angular momentum of the spherical mass in question are zero. Hence the body described by the solution has no rotation. As nearly all astrophysical bodies have rotation then a solution to the equations of General Relativity which describes a spacetime where the angular momentum of the body’s mass is accounted for was long desired.
To say the mathematics in order to find solutions to General Relativity is insanely complex would be an understatement in my opinion. It may have taken Schwarzschild only a couple of months to find the simplest case but it took until 1963, a near half-a-century later, to find a solution that described rotation. It was Roy Kerr who in 1963 managed to finally solve the equations in order to produce the solution that has become known as the Kerr Metric. [38]
The Kerr metric describes the geometry of spacetime in the vicinity of a mass \(M\) rotating with angular momentum \(J\). The metric in Boyer-Lindquist coordinates is
$$ ds^2= -c^2d\tau^2 = -(1-\frac{r_sr}{\Sigma})c^2dt^2 +\frac\Sigma\Delta dr^2 + \Sigma d\theta^2 + (r^2+a^2+\frac{r_sra^2}{\Sigma}sin^2\theta) sin^2\theta d\phi^2 - \frac{2r_srasin^2\theta}{\Sigma} cdtd\phi \phantom{xxxxxxxxx}(6) $$
where the coordinates \(r, \theta, \phi\) are standard oblate spheroidal coordinates and for brevity:
$$ a=\frac{J}{Mc}\phantom{xxxxxxxxx}(7) $$ $$ \Sigma=r^2+a^2cos^2\theta \phantom{xxxxxxxxx}(8) $$ $$ \Delta=r^2-r_sr+a^2\phantom{xxxxxxxxx}(9) $$
where \(r_s\) is the Schwarzschild radius defined in equation (3). Off course, if you’re thinking “Is that what they found written on the crashed alien ship at Roswell?”, I can’t blame you. But to get an understanding of the history and components of this solution there is this very illuminating lecture given by Roy Kerr, from 2016, at the University of Canterbury, Christchurch [39]
Lecture by Roy Kerr about his metric and its mathematical discovery, by him, as the Crafoord Laureate 2016 at the University of Canterbury, Christchurch. [39]
With the discovery of the Kerr metric a new anatomical structure to black hole solutions was given form. This form is given shape externally in the way the fabric of spacetime is dragged rotationally along by a given body. Known as rotational frame-dragging the best way, I find, to visualise this effect comes in seeing the vortex flow of water in a whirlpool as it is poured down a drain. In fact, an analogue experimental method to studying rotational black holes comes from watching water pour down a drain. [40]
A key reason why fluid mechanics is used as an analog model is that solutions to Einstein’s Field Equations, particularly the Friedmann-Lemaître-Robertson-Walker (FLRW) metric, where spacetime are spherically symmetric and conformally flat must contain a energy-momentum tensor of perfect fluid type. Hence the use water, a fluid, as an analog to the fabric of spacetime.
Without rotation the water flows straight done the drain. This can be seen as an analog model of a Schwarzschild, non-rotating, black hole. With rotation a vortex or whirlpool shape is formed. This can be seen as an analog model of a Kerr, rotating, black hole. In fact fluid vortices are actually used as an analog model in studying rotating black holes like this experiment by the Quantum Gravity Laboratory. [40] [41] [42]
So as an analog to a non-rotating black hole, as described by the Schwarzschild metric, this video shows the flow of water straight down a very large drain hole at Monticello Dam. Here the flow of water is uniformly inwards towards the centre of the pipe. That is each streamline points in towards the centre and whose vector is perpendicular to the circumference of a pipe. The closer to the pipe’s opening the faster the flow of water becomes such that it continues to accelerate until it is fully pulled over the edge and in free fall.
In comparison this video shows rotation in the fluid as it flows down a drain and is itself an actual analog experimental setup for studying rotating black holes. Here the streamlines spiral in towards the centre; as opposed to being a straight line. Notice also how the gradient curvature of the streamline increases the closer it gets to falling down the drain. The closer the water is to falling into the drain the greater it’s rate of rotation. In effect, an inner region is dragged at a faster velocity than an outer region.[40] [42]
One approach that helps me to under General Relativity is to realise that the reason I am pulled and stuck to the Earth is because the rate at which a clock ticks at my feet is slower than one ticking at the level of my head. To say, the effect we call gravity is manifested by the difference in the rate at which time passes coming from the inertial mass of a given body. Here on Earth that difference between the rates of time at both my feet and head is nearly undetectable; a trillionth of second over a lifetime. Close to a black hole the effects are far more extreme.
With this said another way to imagine rotational frame dragging is to picture an ice skater orbiting at the equator of rotational black hole. The skater, arms at her sides, is north-south orientated and rotationally at rest with respect to the stars. The skater then extends her arms.
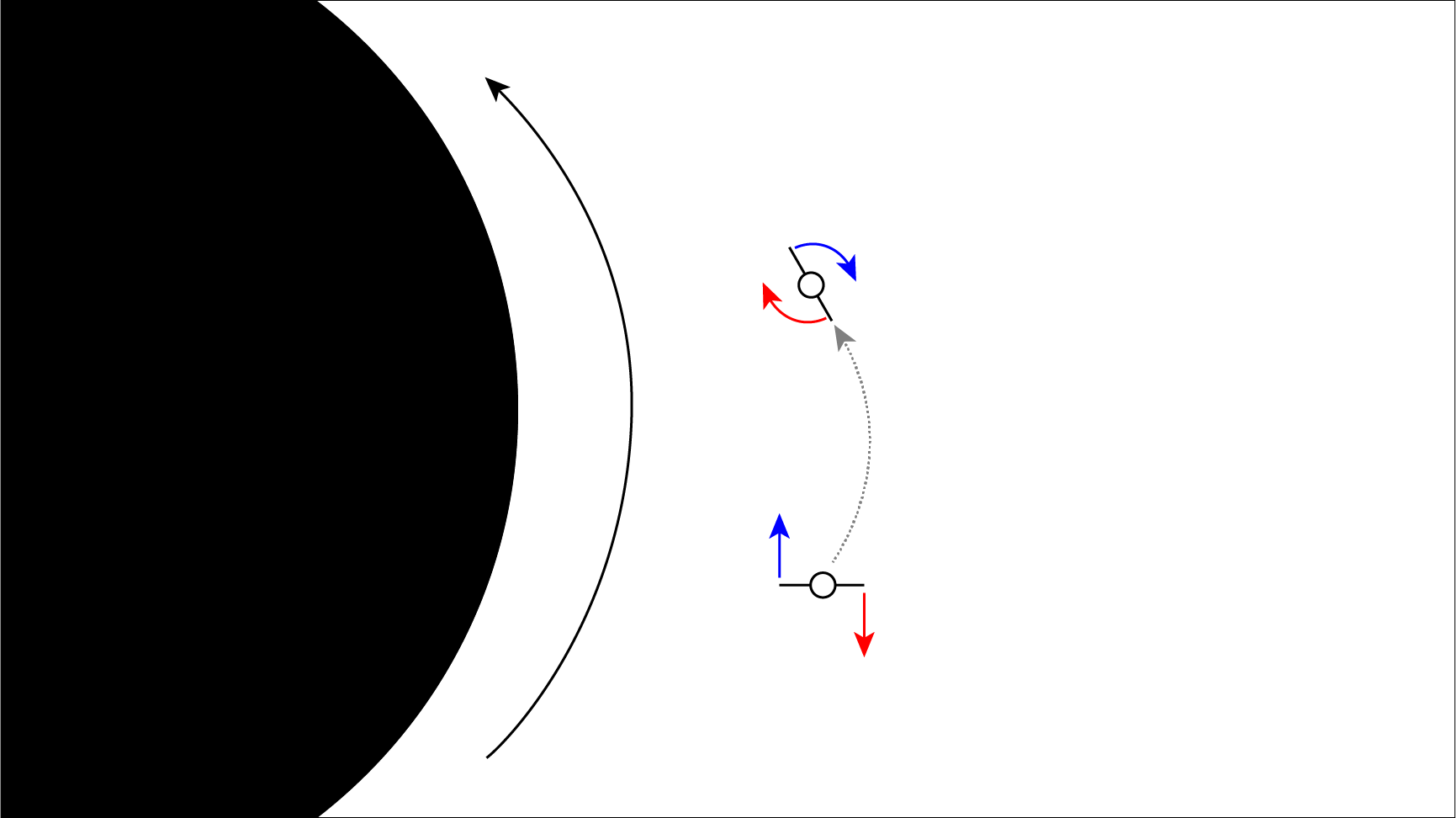
Looking down upon the skater, her arms extended, orbits a black hole whose spinward direction is anti-clockwise. The blue arrow shows the torque force in the anti-clockwise spinward direction. The red arrow shows the torque force in the clockwise anti-spinward direction. In effect, the skater is spun in a clockwise direction which is counter to the anti-clockwise direction of rotation of the given black hole.
The arm extended towards the black hole will experience a torques force spinwards; the flow of time being slower relative to her body. Likewise the arm extended away from the black hole will be torqued anti-spinward; the flow of time being faster relative to her body. She will therefore be rotationally sped up, in a counter-rotating sense to the black hole. This induction of torque rotation comes from the dragging of spacetime at different rates where an inner region is dragged at a faster rate than an outer region.
In researching this work one sentence stands out in relation to describing rotational frame dragging. To quote, “Qualitatively, frame-dragging can be viewed as the gravitational analog of electromagnetic induction”.
The first reason this stands out is because I’ve been trying to envision light in the Superverse. Light is given form by the photon and this is the force particle of the electromagnetic force inside our universe. So what is the equivalent force particle that lights the Superverse?
In trying to picture this I am led by my rule of thumb; “Gravity-time is equivalent to the electro-magnetic force, but on the next scale up”. I particularly laid out the concept in demonstrating my first computational model whose behaviour is given form as a matter of electromagnetic induction within a model containing a single magnetic field.
Further to this in describing the specifics of a hypernova we saw how the increased rotation of plasma, driven and accelerated by the collapsing core, generates a solenoid shaped electromagnetic field. It is this field, due to its shear strength, that shapes the jets via electromagnetic induction. However in the hypernova essay I also noted that General Relativity has a part to play as well. This part, discussed below, is seen in the Penrose Process and the effect of superradiance which are a direct consequence of rotational frame dragging and jet formation.
The second reason this stands out is because a critical argument that the Big Bang Hypernova Hypothesis looks to make is to say that CPT-Symmetry is not a fundamental law of nature. Rather it is law which is given physical shape by the formation of the jets in the Big Bang Hypernova. More fundamentally, as a physicist, I am looking to try and answer the question “What is a field? Be it gravitational or quantum, what makes it?”. Employing the lens of fractal geometry and scale invariance I view that which is to us both gravity and time as being equivalent to the electro-magnetic force within the Superverse.
However, the specifics of this idea particularly focus on the speed of light inside a Bose-Einstein Condensate being only 17 metres per second. In short, extending from my logic that “Black Holes are fundamental particles” I looked to understand what the effect rotation has in a superfluid where such condensates could form. Although the real credit for this inspiration comes from Eric Laithwaite’s work. Putting these two together was what led me to Martin Tajmar’s experiment demonstrating rotational frame-dragging in a lab. [43] [44] [45]
Or as I phrase it, “OH MY GOD!!!! THAT’S IT! THAT’S FRAME-DRAGGING IN A LAB!!! WHY OH WHY IS NO ONE REPRODUCING THIS EXPERIMENT?”, all the while arming the largest cattle-prod that divinity has ever seen in order to apply for a research grant. To be honest, I consider this has the potential to be the single most important scientific experiment in all of humanities history. To see why let us consider a first applicational use.
So how do we solve Global Warming and the Energy Crisis?
Tokamak fusion reactors employ liquid helium for induction of a magnetic field in which the plasma is contained. With just the right rotation, shape and flow of the liquid helium the electro-magnetic force can be temporally “extended” such that it bends spacetime within the reactor’s chamber. This artificial man-made curvature is a kin to the curvature of spacetime inside a star. Thus we are able to hold and shape the unstable plasma inside the Tokamak fusion reactor in order to create a sustained fusion reaction.
Or in Green speak, a completely renewable and sustainable energy source without any Carbon Dioxide or other pollution. The helium by-product from the fusion can be re-cycled either for frame-dragging applications or so I can inflate a balloon before saying the magic words “Warp Drive!!!!”. The kid that wanted to be Luke in me comes alive.
But before we can fully realise the applicational uses that this hypothesis might bear fruit too we need to return back to our discussion in regards to frame-dragging in the context of a rotational black hole.
With rotational frame-dragging the frame of reference, as viewed by a distant observer, in which a clock ticks the fastest is the one which is revolving in the spinward direction of the astrophysical body. This implies that light traveling in the direction of rotation of the astrophysical body will move past the body faster than light moving against its rotation, as witnessed by a distant observer.
This effect of rotational frame-dragging was key in the experimental confirmation, via the Gravity Probe B experiment, of this phenomena, as predicted by General Relativity. Truly one of the hardest and greatest scientific experiments ever done by humankind, in my humble opinion. [46]
Ultimately, for a rotational black hole, this effect of frame-dragging means that any particle that falls in towards said black hole will be forced to follow its rotational direction. So imagine a particle whose initial direction of rotation is counter to that of the black hole’s direction of rotation. As the particle falls in towards the black hole then because of the effects of frame-dragging the rotational direction of the particle changes such that it eventually travels in the spinward direction following the black hole’s direction of rotation.
In considering light and the orbital direction of a photon falling into a rotating black hole it allows us to define the region around a rotating black hole called the Ergosphere.
The Ergosphere is seen as a region outside the event horizon, given sufficient spin, of a rotating black hole. A photon, on the surface of the Ergosphere, whose direction of travel is counter to the rotation of the given black hole’s direction rotation is seen as being stationary by a distant observer. Nothing inside the Ergosphere will be seen as stationary, by a distant observer, because of the magnitude of the inertial frame-dragging arising from the black hole’s rotation. An object would have to be travelling faster than the speed of light if it were to be seen as stationary inside the Ergosphere and Special Relativity denies this.
The Ergosphere gets its name from the Greek word “ἔργον” (ergon) which means “work”. The reason being that it is theoretically possible to extract energy and mass from this region. The famous example of this being the Penrose Process. [47]
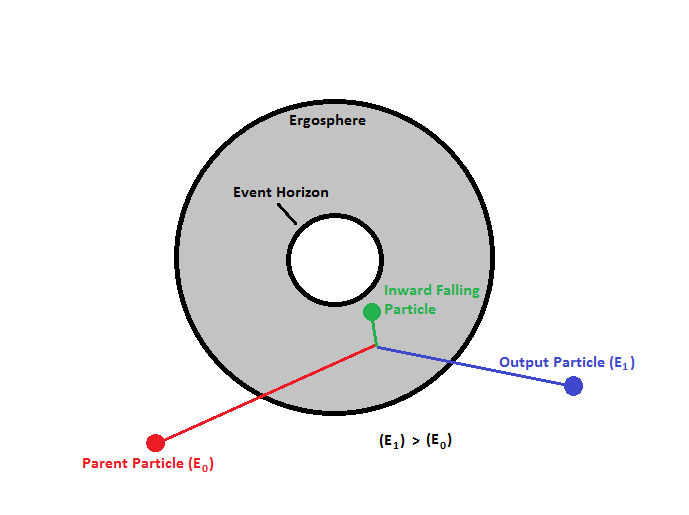
The Penrose Process works by extracting the energy from a black hole through use of an intermediary particle. This particle entering the rotating black hole breaks apart by some means sending one piece into the event horizon and the other out of the ergosphere with more energy than it originated with. [48]
Once inside the Ergosphere the same kind of pattern of behaviour as we saw when describing falling through the event horizon of a non-rotating, Schwarzschild, black hole is now applied. In a non-rotating black hole both the spatial and temporal dimensions change roles. Space becomes time and time becomes a uni-directional spatial dimension. However, the key difference inside the Ergosphere is that rather than space being swapped it is one of the angular coordinates. So rather time becomes angle and angle becomes time.
As a mathematician such a thing can look like a clever trick in solving the equations. But as discussed, particularly in light of Eben Alexander’s testimony, there is something truly mysterious about the nature of reality crying out to be discovered here. Angles and their preservation, conformal mapping, is fundamental to the existence of Fields; be it gravitational or quantum. Penrose himself has developed his Cyclic Conformal Cosmology model where the word conformal means angle preserving. [15] [49]
Further to this is the X17 particle experiment where the angle between the ejected electron and positron pair is at an angle of \(140^\circ\). Here we see the X17 a photophobic boson that has been described as being a “fifth fundamental force”. Now remember that a key part in identifying the pattern of nature that we should study in developing the Big Bang Hypernova Hypothesis comes from electron/positron annihilation and its ejection of gamma-rays at \(180^\circ\). Here in the X17 experiment I am seeing the potential idea of making our own quantum fields. Say like the “emergency containment force-fields” that seem to populates nearly every episode of Star Trek. [50] [51]
Now here we see the importance of angles inside the Ergosphere. However one of the main argument that I am trying to put on the table is how a causally and continuously closed vacuum space inside a Lorentz manifold, or verse, is the ultimate product of a rotating and charged black hole. How this happens is the fundamental question I am trying to explore. And so, what may appear as a small detail in explaining the Penrose process and the Ergosphere is to my eyes is an extremely important clue.
My spine tingles, senses heightened, Apollo closes upon His prey.
For the Penrose Process, in terms of the mathematics, this unusual coordinate swap between angle and time means that the total mass-energy of the rocket can become either both a positive or negative value; as measured by an observer at infinity. What a negative energy value, associated to the rocket, implies is that this energy debt is paid for by the energy coming from the angular momentum of the rotating black hole’s mass.
Our rocket, inside the Ergosphere, and with the fuel expended in its first stage; now separates and the second stage rocket fires. The first stage will fall away to be lost forever as it crosses the event horizon. The second stage craft, whose rocket is now firing, will escape the Ergosphere.
The trick in the Penrose Process, in order to extract energy from the rotating black hole, comes in choosing just the right point at which to separate the rockets such that the escaping craft has a greater mass-energy than the original two stage rocket before it entered the Ergosphere. The mass-energy of the in-falling first stage rocket becomes negative which is counter-balanced by the escaping craft gaining greater kinetic energy. Thus the escaping craft, which has been accelerated to relativistic speeds in order to escape the Ergosphere, has a greater mass-energy value than the original rocket before the process began.
The Penrose Process when applied to light is called superradiance. With superradiance a photon, travelling in the spinward direction of the black hole, enters the Ergosphere. Energy coming from the angular momentum of the rotating black hole is imparted to the photon such that when it escapes the Ergosphere the photon’s wavelength has decreased; hence its energy has increased. Here powerful X-rays are supercharged into becoming gamma rays; as in the gamma rays of the gamma ray bursts. Examples of superradiance are Zel'dovich radiation and Unruh radiation. [52] [53]
The anatomy of a rotating black hole is broken into a number of different horizons. With reference to Matt Visser’s description of the Kerr metric a rotating black hole can be divided into a series of regions each separated by a given surface. The table below lists each of these regions along with the equation that defines its surface. Here the parameter \(m\) is the physical mass of the black hole and parameter \(a\) is the ratio rate of rotational spin as defined by equation (7). [54]
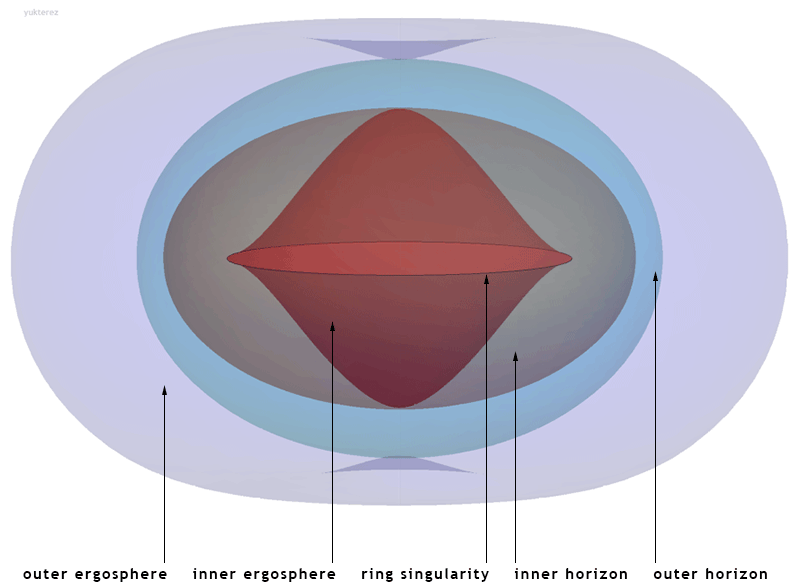
Location of the horizons, ergospheres and the ring singularity of the Kerr spacetime in Cartesian Kerr-Schild coordinates. [54]
Starting from the outside and moving inwards; the first region we encounter is the Outer Ergosphere. The Ergosphere, as we have just discussed, or more accurately the Outer Ergosphere is the region lying outside the Outer Event Horizon. A photon of light on the surface of the Outer Ergosphere whose direction of travel is anti-spinward to the spinward rotational direction of the black hole will appear to a distant observer as being stationary.
| Outer Ergosphere | \(r^+_E=m+\sqrt{m^2-a^2cos^2\theta}\) |
|---|---|
| Outer Event Horizon | \(r_+=m+\sqrt{m^2-a^2}\) |
| Inner Event Horizon | \(r_-=m-\sqrt{m^2-a^2}\) |
| Inner Ergosphere | \(r^-_E=m-\sqrt{m^2-a^2cos^2\theta}\) |
| Ring Singularity | \(x^2+y^2=a^2\) and \(z=0\) |
The next region we encounter is the Outer Event Horizon which is the point of no return. Just like the event horizon of a Schwarzschild black hole; the escape velocity from the black hole at the surface of the Outer Event Horizon is equal to the speed of light.
On the other side of the Outer Event Horizon we next encounter both the Inner Event Horizon followed by the Inner Ergosphere. However in order to understand these horizons we will need to unpack the full Kerr solution in the context of a Penrose Diagram. But before we can do this we need to have a careful discussion about the gravitational singularity that is no longer a point but is instead a ring; the Ringularity.
A gravitational singularity is described as being a location where the curvature of spacetime has become infinite. In the case of the Schwarzschild black hole the singularity is described as being a point of infinite density, at \(r=0\), which thus causes the curvature of spacetime to become infinite at this point.
However with rotation this singularity becomes a ringularity. This ring where the curvature of spacetime becomes infinite drastically changes the theoretical outcome. Rather than the universe coming to an end at an infinitely dense point, as we shall see, the ringularity along with the inner event horizon rather acts to create a wormhole which leads to a new universe via a white hole.
Strictly speaking, from a mathematical point of view, a ringularity will always form within a black hole unless there is exactly zero rotation. From the equation of the ringularity we see that \(x^2+y^2=0\) if and only if \(a=0\). This thus implies that a point singularity can only exist if and only if there is exactly zero rotation.
In previous work I have highlighted how we see rotation in everything from the spin of quantum particles, up through the scales, to the rotation of galaxies. Off particular note, I have discussed how the rotational velocity of a collapsing core in a dying star is exponentially accelerated. So the idea that an actual physical Schwarzschild black hole, with no rotation, could be even be born in the heart of a hypernova is considered to be completely unrealistic. The collapsing star would have to be perfectly spherical with absolutely no angular momentum.
But what about the Big Bang itself? Hawking showed in his Phd thesis, by employing Penrose’s newly developed Singularity Theorem, that the Big Bang must have come from a gravitational singularity. In the half century since that discovery the idea of Cosmic Inflation has come to dominate the discussion in describing the exact specifics of what happened inside the Big Bang event itself. The very description given to us by Cosmic Inflation specifically describes how an infinitely small but infinitely dense point singularity underwent exponential expansion in the picoseconds following its birth. [9] [32]
To understand this we need to talk about another exact solution of Einstein’s Field Equations.
The Friedmann–Lemaître–Robertson–Walker (FLRW) metric is the standard model of cosmology and is an exact solution of Einstein’s Field Equations. Developed independently by Alexander Friedmann, Georges Lemaître, Howard Robertson and Arthur Geoffrey Walker in the 1920’s and 30s this metric is the key cornerstone of virtually all cosmology. Spacetime as described by the FLRW metric is both spherically symmetric and conformally flat.
The FLRW metric is the very mathematical embodiment of the cosmological principle that the universe is, at the largest scale, both homogenous and isotropic. It describes an expanding path-connected geometry of spacetime where the distribution of the mass-energy density is both homogenous and isotropic.
In my Expansion of Spacetime film we explore the history and development of the Big Bang theory.
As I discussed in my Expansion of Spacetime film it was both Alexander Friedmann and Georges Lemaître who first realised that the universe was in fact expanding. Lemaître himself is credited as being the original progenitor of the Big Bang theory itself. A prediction made in order to test this theory came in realising that the afterglow of the Big Bang should be seen coming from every heavenly direction. This afterglow which we now call the Cosmic Microwave Background Radiation was actually detected and measured. The prediction and subsequent discovery of this afterglow comes as a direct consequence of the FLRW metric. Thus the FLRW metric cemented its reputation and is described as being the standard model of cosmology.
Now Penrose’s Singularity Theorem used both the Schwarzschild and Kerr metrics in order to show that given sufficient conditions that it is not just possible but inevitable that the collapsing-core of a massive dying star will give birth to a black hole and its associated singularity. So this theorem only applies to massive stars. [23]
Steven Hawking, on the other hand, employed the FLRW metric in taking Penrose’s ideas in order to see if the Big Bang came from a gravitational singularity. Here the FLRW metric is used as a “scaling” factor in order to describe the shape and size of the observable universe. Then by running the clock back Hawking showed that by using the FLRW metric all the matter and energy in the universe came from a single infinitely dense point. [55]
The key idea I am trying to communicate is to question this very assumption that the Big Bang singularity was indeed a point singularity. As we have seen, in talking about the Schwarzschild and Kerr metrics, gravitational singularities in realistic black holes are in fact ring shaped ringularities. The reason this is important is the story told by a ringularity in a black hole is completely different to the point singularity, as we shall later discuss.
In the Big Bang Hypernova Hypothesis we know that rotation is critical in the formation of a hypernova. Without rotation there is no accelerated rotation of charged plasma which induces a solenoid shaped magnetic field that acts to shape the jets in a hypernova. We view the collapsing-core of the MacLean in the Superverse as equivalent to a Kerr black hole being born. Thus the gravitational singularity in the context of my hypothesis is a ringularity.
An obvious line of thought would be to ask, “What is the shape of a singularity given the FLRW metric also accounted for rotation?”. Well as I just mentioned the region of spacetime in the collapsing-core of the MacLean follows the Kerr metric. By looking at the extended solution we’ll see how a new universe, like ours, comes to exist. On the other hand I would like to know if rotation creates a ringularity when applied to the FLRW metric?
It must be recognised that the FLRW metric is a greatly simplified solution to Einstein’s Field Equations which was developed in the 1920s and 30s. The Kerr metric which accounts for rotation proved to be much more complicated to solve and was only finally solved in the 1960s. But to this end a modified FLRW metric has been developed that does in fact account for rotation. So an interesting line of enquiry! [56]
Having mentioned Cosmic Inflation and the assumption of a point singularity I think it is very important to look at the state of affairs within modern physics. On the one hand, the scientific establishment will put on a respectable unified front in claiming that they can describe the creation of our universe to within \(10^{-50}\) of a second. On the other hand, I think the vast majority of physicists don’t even believe in the concept of a singularity. Our proposed solution, as written as a mathematical formula, is not complete or there is something missing in our understanding.
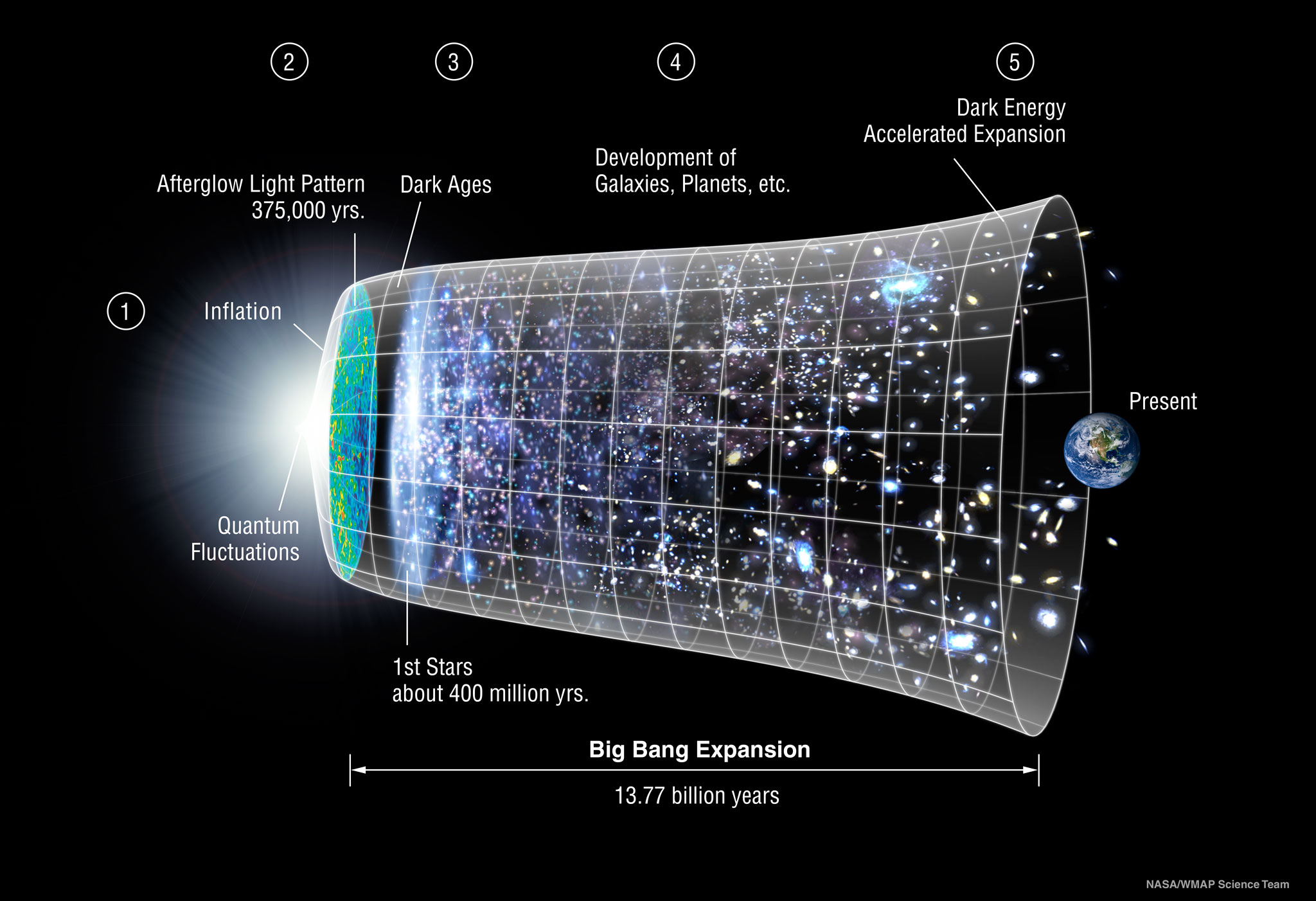
Graphical depiction showing the Lambda-CDM model of our expanding universe. Is it just me with my bias or does this famous graphic by NASA’s Lambda team look like an expanding unidirectional jet originating from a single source point? Thank you team Lambda for the graphic that helps make my case. Sorry to team Lambda for what now follows as I tear your precious model apart. [57]
The Lambda-CDM model is currently the main standard model of cosmology. Cosmic Inflation and the FLRW metric are integral parts of that model. But the FLRW metric and hence General Relativity are only really employed as a means in order to find the “scale” of the universe. How matter interacts and behaves in the Lambda-CDM model is governed by Quantum Field Theory. This is most particular when dealing with model’s of the very early universe, around the Inflationary Epoch, where the entire universe is itself at the quantum scale. [57]
Since Einstein, physicists have looked to try and unify the four fundamental forces of nature in the context of Quantum Mechanics. Namely to unify the four fundamental forces being the strong nuclear, weak nuclear, electromagnetic and gravitational forces. This unification of force happens under very high energy and temperature conditions. Particle Accelerators like Fermilab and the Large Hadron Collider are used to create such high-energy conditions. [58]
The most successful example of successfully showing the unification of force comes with the discovery of the Higgs Boson. The theoretical Higgs field first being proposed in looking at how the weak nuclear and electromagnetic force both unify into the electro-weak force. Further to this the electro-weak force will unify with the strong nuclear force given even higher temperatures. The last force to be unified is gravity and this line of research is called Quantum Gravity. [59]
With respect to the Big Bang this unification of forces happens as one gets closer to the very moment of creation; when the Big Bang point singularity came into existence. The closer to the moment of creation the higher the temperatures leading to a unification of forces. We know about the unification of all the forces, from particle accelerators, with the exception of gravity which is believed to happen when the universe was younger than \(10^{-50}\) of a second. Hence this is where this statement comes from.
In terms of the Big Bang Hypernova Hypothesis the unification of forces is seen in the unfolding of the jet into a series of concentric rings. It is also the lines within the central pillar of my inspirational artwork and now logo. Shame the original artist got nailed up by the patron of this piece for his other work. But that’s just life!
The massive elephant in the room in regards to using Quantum Mechanics as a foundational basis comes with how it tells us how matter came to exist in the first place. As we know from Quantum Mechanics, the creation of matter requires an equal amount of antimatter to be created as well.
The logical consequence of this fact being that in order for the Big Bang point singularity to appear then it most produces both equal amounts of matter and antimatter. Matter and antimatter when brought together annihilate each other as we can see from the reaction of positrons and electrons. As equal amounts of matter and antimatter are in close proximity to one another, being contained inside an almost infinitely dense point, they naturally annihilate each other. Now this all happens at around \(10^{-50}\) of a second after the Big Bang singularity has appeared. [60]
Matter and antimatter annihilation is the single most high energy reaction that we know off. A good example being pair-instability supernovae where antimatter is produced during core-collapse that effectively annihilates the matter of the collapsing core. It is an explosion more powerful than even a hypernova and no remnant of the collapsed core, such as a black hole, exists.
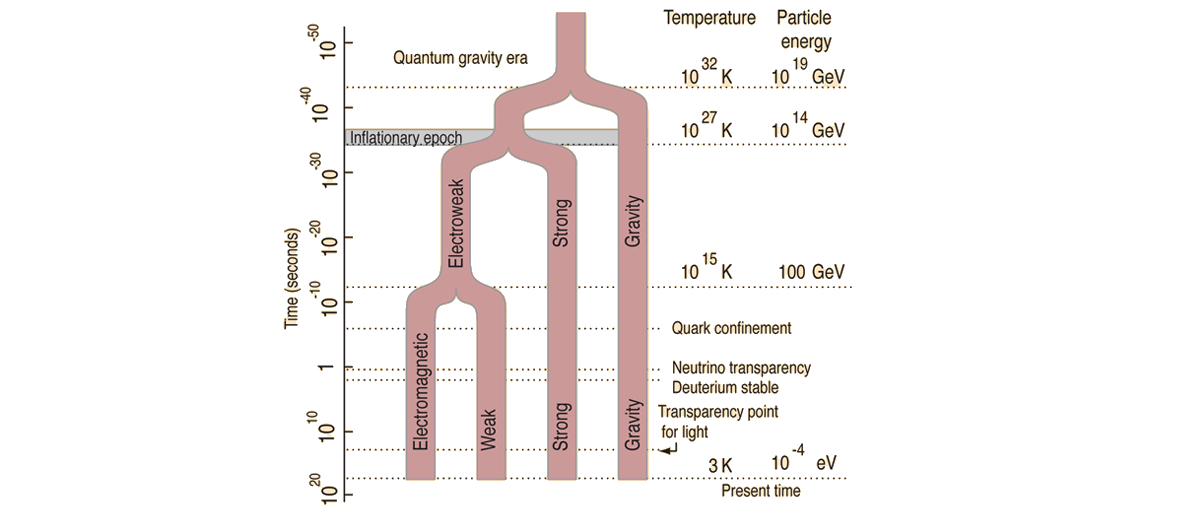
Illustration showing the unification of the four fundamental forces and their associated timing in the context of the Lambda-CDM Big Bang model. [61]
The caveat as to why the universe did not just annihilate itself completely in the first \(10^{-36}\) of a second comes from experimental evidence which shows a slight imbalance in the symmetry between kaon and anti-kaon particles. Known as Baryon Asymmetry this slight imbalance, from experiments of kaons, implies that about only a billionth of the original matter remained after all the antimatter was annihilated.
The period between \(10^{-36}\) and \(10^{-32}\) of a second since the moment of creation is called the Inflationary Epoch and is the part in the Lambda-CDM’s story where the idea of Cosmic Inflation applies. Now Inflation Theory was invented in order to try and resolve a massive problem in the Big Bang theory; one which arises from considering the Second Law of Thermodynamics.
The second law of thermodynamics says that the unidirectional arrow of time moves a system from order to disorder as entropy increases. Thus it is logical to assume that the universe was at its most ordered state the very moment the Big Bang singularity came into existence and time began. The goal of Inflation Theory was to answer the question how did the Big Bang give birth to a universe where the laws of physics and constants are the same all over. Namely we see a mostly homogenous and isotropic universe where galaxies look the same in every direction.
The alternative view of imaging the Big Bang, coming from an infinitely small point, as the hottest and most chaotic explosion only led to the conclusion that the universe would either blow itself up completely or collapse back in on itself. Either way the result is exactly the same being total oblivion. We know the universe exists because we live inside it and can see it. A universe whose constants are so finely-tuned that the probability, to quote Roger Penrose, of its existence coming from such an infinitely small point is:
$$ 1 : 10,000,000,000^{237} $$
Which is still a small number when compared to infinity. [62]
Beyond this debate is the debate how the Big Bang singularity came to exist in the first place. Many see the universal constants of physics as being finely-tuned as if it is not an accident. This is called the anthropic principle and is basically the evolution of the oldest conversation known to humanity in looking for a divine creator. It is also the reason why I guess many physicist lower their standards in making excuses for the following paradox.
Because the second law of thermodynamics tells us the universe moves towards increasing disorder then it is completely reasonable to arrange the mathematical description in a perfectly ordered state. To this end Inflation Theory begins its description of the universe as being perfectly spherical whose distribution of mass-energy is constant at every single point within the volume of the sphere. That is the universe at \(10^{-36}\) seconds after the Big Bang is described as being perfectly spherical having perfect homogenous and perfect isotropic distribution of matter. Inflation theory then goes onto describe how the “inflation” field exponentially expanded the universe and how “quantum fluctuation” caused the distribution of the remaining matter to be perturbed.
Now as we’ve just discussed before \(10^{-36}\) seconds we have the annihilation of almost all matter and antimatter. Only a billionth of the original whole remains. But yet the universe just after the single most explosive event in the universe is described as being perfectly spherical, homogenous and isotropic. To say this is a bit of a contradiction or paradox would be to put very politely. I more have a look that says, “What the hell have you been smoking and can I have some?”; believe me the way I’ve had to bend my mind it becomes a requirement.
Here is another question that arises from this paradox. Given that only a billionth of the original whole remained then it logically implies that all this matter and antimatter was converted into energy. However the Lambda-CDM model says that 4.6% of the universe is made from normal matter and 24% is dark matter. But the annihilation of all but a billionth implies that only 0.0000001% should in fact be matter and the rest energy. Again another paradox! [63]
Ultimately it puts a physicist in a very tight spot. On the one hand the story told by the Lambda-CDM model is led by the best science and understanding. On the other it is because of these contradictions that no real physicist actually buys this explanation.
And all of this comes down to what I think are two very critical mistakes. Firstly, the assumption that the Big Bang came from a single point singularity. Secondly, we should be looking towards General Relativity, as opposed to Quantum Mechanics, to actually understand the Big Bang. After all, the Big Bang theory is itself a prediction arising from General Relativity.
The main focus of my CPT-Symmetry in the Superverse work was to show how a hypernova
gives rise to a series of CPT-Symmetric
Returning to our discussion of rotation I look to answer the mysteries of the Big Bang by understanding the ringularity. Having just lampooned the idea of a point singularity in order to replace it with a ringularity then I feel the onus is upon me to test this new assumption. This assumption of a ringularity is thus predicated that the universe, at the largest scales, itself must have rotation.
“So what evidence do I have for a rotating universe?”, a Cheshire Cat’s grin appearing upon my face. The answer has been staring us in the face ever since COBE’s first map of the Microwave Sky. However before we get there we need to complete our discussion in regards to the Kerr metric and rotating-black holes. Only by this are we able to start talking about the overall structure and metric of a spacetime as described by the Big Bang Hypernova Hypothesis.
In order to see the behaviour inside a rotating black hole we need to look at the extended Penrose Diagram showing a Kerr spacetime geometry. [2]
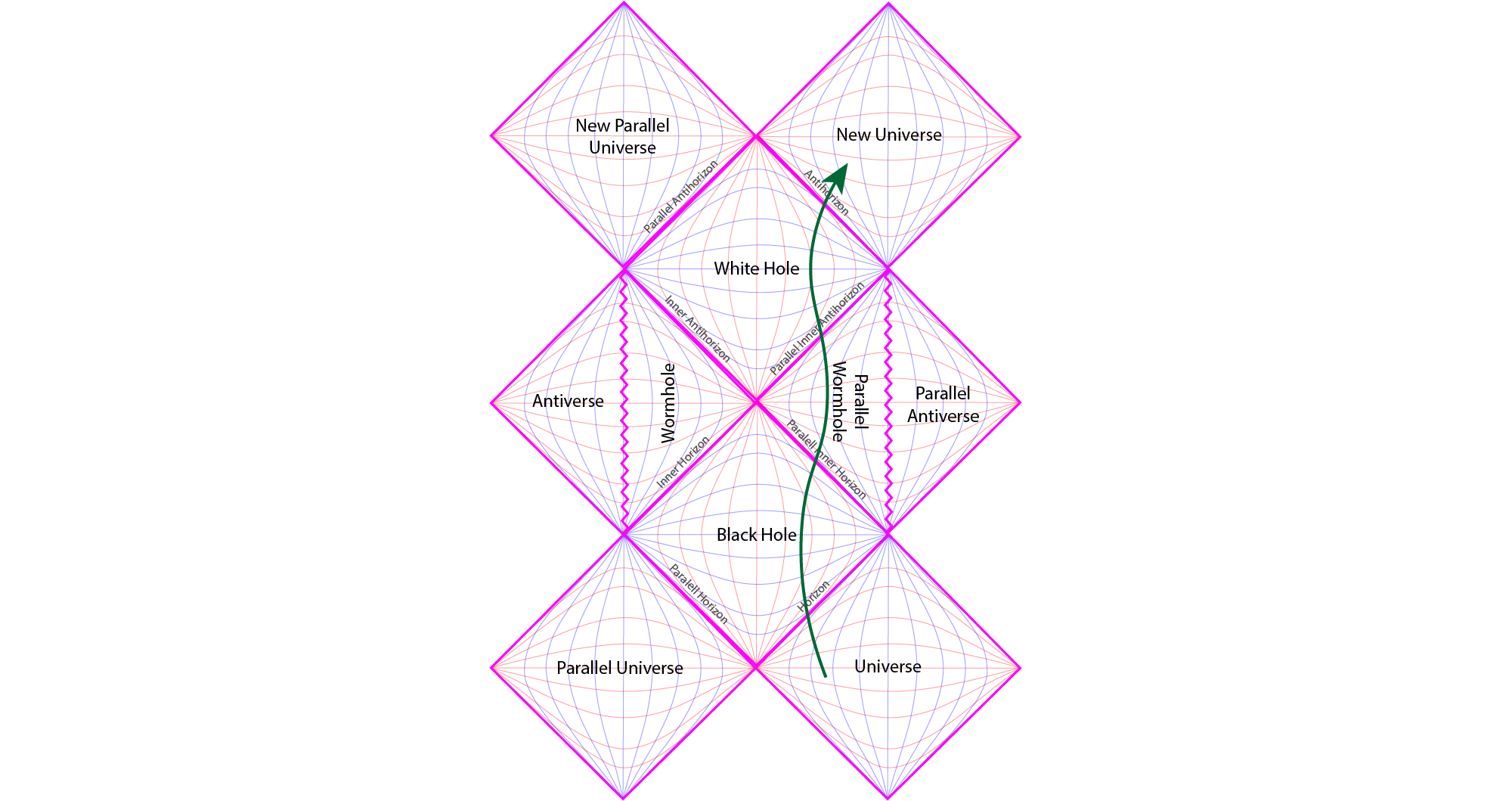
The maximally extended Penrose Diagram of rotating black hole following the Kerr metric. Following the path of a particle, marked by the dark green line, we start our journey inside our own universe falling into the rotating black hole. Crossing over the Outer Event Horizon we fall through the time-geodesic volume and into the Wormhole at the centre of the black hole. Passing through the wormhole our particle then traverses the White Hole and out into a New Universe.
Like the Schwarzschild extended Penrose Diagram; the Kerr extended Penrose Diagram shows both our universe and a parallel universe. From looking at CPT-Symmetry, a fundamental property of quantum field theory, we see that General Relativity is also telling the exact same story about their being a parallel universe to our own. In the context of the Big Bang Hypernova Hypothesis each verse arises from the output of the two jets; two Jet-a-verses. But only in the context of this Penrose Diagram are we finally able to see exactly why these output jets are universes in their own right.
Falling into a Kerr black hole we follow the dark green line down from our universe passing in through the outer ergosphere which is defined by the black hole’s rotation. As we discussed, anything inside the ergosphere will be seen to follow the black hole’s rotation. A photon on the surface of the outer ergosphere whose direction is counter to the black hole’s rotation will seen to be stationary when observed at a distance from the black hole.
Crossing over the outer event horizon we pass the point of no return. Like the event horizon of a Schwarzschild black hole the escape velocity at the outer event horizon is equal to the speed of light. Here the metric of both space and time are reduced to zero at the horizon where they then swap roles. The 3-dimensions of space and 1-unidirectional dimension of time, called a space-geodesic, swap roles giving us 3-dimensions of time and a single unidirectional dimension of space which we call a time-geodesic.
Travelling further down we encounter a very strange place as we cross the inner event horizon. Known as a Cauchy horizon and like the outer event horizon the role of dimensions are again swapped. The time-geodesic becomes a very strange space-geodesic called the Wormhole. Here in the wormhole as cause no longer necessarily precedes effect as the past no longer necessarily determines the future. [64]
Now the problem with wormholes, in the human psyche, is that since their conception they have been viewed as bridges in spacetime. Or rather, we view wormholes as allowing us to cross vast interstellar distances. But let us really think about the specifics of a wormhole inside a black hole born from the collapsed core of a dying star. By Penrose’s Singularity Theorem the reason the singularity inside a black hole even forms is because every geodesic path inside the Schwarzschild radius leads down to the singularity. My point being that being bounded and contained from its birth the exit of the wormhole does not just magically appear on the other side of the galaxy like in Star Trek’s DSN9. Rather the exit from the wormhole is bounded inside the spherical volume as defined by the Schwarzschild radius. [23]
However the view given by science fiction is rather pale in comparison to what the extended Penrose diagram of Kerr black hole is telling us. Following the path of an object past the inner event horizon it passes on through the wormhole crossing over the inner anti-horizon of a rotating White Hole.
We saw earlier that the Schwarzschild white hole was in effect a time-reversed Schwarzschild black hole. The Kerr white hole in effect is a time-reversed Kerr black hole. Here our object travels out from the White Hole and into a New Universe. Vice versa, we could alternatively come out of the White Hole and into the New Parallel Universe. This is the logical consequences following rigorous mathematical analysis coming from studying the Kerr solution of General Relativity.
Before we see how these twin pair of universes actually manifest themselves in the context of the Big Bang Hypernova Hypothesis I feel proper description of the wormhole inside a rotating black hole has not fully been given. This is not a place a spacecraft can simply fly through and remain intact. More it is a place where such a craft would not just be torn apart down to the atom but the very atoms themselves would be torn apart and transformed. One might even be tempted to quite literally call it Hell.

On the left, is a diagram showing a Tibetan Cosmological Model. On the right, depiction from the Arch of Titus of the Romans looting the Temple Mount. In the middle, the coffin of the Temple Mount’s former management which in totality passes as a most humorous joke between one avatar and another His kind. Note that each has a scaled base with a series of four steps. Also in the middle picture of the slightly inconvenient ANOMALY the clockwise and anti-clockwise spirals which I’ll use later in this piece in order to explain rotation and the anisotropies of the CMB. Why oh why didn’t I just take the blue pill! [65] [666]
Funny thing, it was just this vision of Hell that spurned this actual essay. The vision being spurned by way of the Tibetan Cosmological Model. Notice the base of the model being a different level of hell: Hell of Great Darkness, Hell of Endless Smoke, Hell of Swamps, Gravel Water Hell. Note how each level of hell is subsequently smaller than the one it stands upon. The jet-a-verse Tibetan’s call Mount Meru. This is an extremely accurate description given physical form in passing through the horizons of a rotating black hole to be reborn as a new Jet-a-verse. [65]
It was seeing the base as a series of steps each smaller than the one upon which it sat that really allowed me see what a black hole is. A black hole will scale transform the Jet-a-verse in which it is born down such that a new twin set of Jet-a-verses are in turn born. This new smaller universe, inheriting the physics of its parent being a scaled down mirror image of its parent. The black hole itself being the scale transformer between Jet-a-verses where fractal geometry is the governing principle.
Going deeper, that base is not just echoed in the Tibetan Cosmological Model but is exactly the same sitting below the jet of creation upon the Caiaphas Ossuary. It is also the hexagonal base of the Hanukkah menorah depicted on the Arch of Titus showing the looting of the Temple Mount. At which point I suddenly get the joke about threading a camel through the eye of a needle while contemplating the ringularity. Not that creating a legal non-entity called “A Corporation” is a get out clause.
Then there is thought, “If I was God and wished to plan an infinite future learning from the mistakes of the infinite past; where would I setup shop?”. Now go and listen to Eben Alexander’s account of the afterlife from his near death experience and think about how the Christian church has banged on and on about Sin. In death our souls learn from the wrongdoing and mistakes we made in life. What is hell to one is heaven to another in the place where justice of life is both fair and equal.
Then there is thought about taken evolution to its most infinite conclusion and what is the result?
As the Lambda-CDM model completely failed to imagine anything outside of its existence such a question about evolution drawn to its most infinite conclusion is mute. It took me about four years of relentless thinking before even coming up with the name Superverse. And that was after developing my ideas around the MacLean and the Bootes Supervoid.
Such was the mental block upon my brain because I had never questioned the assumption that anything outside of our universe could ever be seen or measured. Dark energy when it was first discovered was simply added, along with dark matter, to the equation totalling up the contents of the Big Bang.
After thinking through every plausible alternative I realised the simplest solution was understanding that the cosmological principle is in fact fractal geometry and the role of scale-invariance and recursion. Nature paints my picture as opposed to the wild fantasies of imagination. Seeing the Bootes Supervoid was what allowed me to first see such a massive starlike object as being something actually external to our universe. The Bootes MacLean allowed me to see an object that was sufficiently massive enough to give birth to a pair of Jet-a-verses which exists externally to the Big Bang itself. The Bootes Supervoid did not form from the dark energy of Inflation Theory but rather because our Jet-a-Verse has flown around the MacLean situated there.
So this leads to my recursive analogy of balloons.
Blowing air into a green balloon inflates it. As it inflates with air the volume of the green balloon grows and expands. By falling through the nozzle of the green balloon we come to be inside the volume of the green balloon. Now air from inside the green balloon inflates a red balloon. As the red balloon inflates with air its volume grows such that it occupies a subset of the volume inside the green balloon. By falling through the nozzle of the red balloon we come to be inside its volume. Repeating the process, air from inside the red balloon inflates a blue balloon. So the volume occupied by the inflated blue balloon is a subset of the volume inside the red balloon. Recursively we can continue this cycle of falling inside the volume of subsequent balloons.
Imagine an inflated green balloon floating through the flat vacuum of space. Being small enough, you find yourself floating inside the volume of this large green balloon. Looking down you see in your hand a red balloon. Blowing air into the red balloon you inflate it. With each inhale of breath you draw air from the surrounding volume of air inside the green balloon. Inflating the red balloon, each exhale of air from your lungs forces air into the red balloon causing its volume to grow. When fully inflated the red balloon will occupy a subset of the volume inside the green balloon.
Like Alice, we have a magical potion that shrinks us down in size. Drinking it you shrink so much that you are small enough such that you float into the red balloon through its entrance; the intake nozzle. Thus you now float inside the red balloon which in turn is inside the green balloon.
Pulling a blue balloon from your pocket you begin the process of inflating the blue balloon. The volume of air that comes to occupy the inflated blue balloon is drawn from the volume of air inside the red balloon. Technically the air inside the blue balloon which is itself also inside the red balloon which is in turn inside the green balloon. However the air inside the blue balloon is trapped inside the blue balloon contained within its elastic continuous membrane.
Again we could continue by drinking our shrinking potion such that we end up small enough to be inside the volume of blue balloon. Blow up another balloon and we could continue on recursively down to the infinity small. Balloon inside another balloon; each one occupying a subset of the volume of its parent.
This recursive analogy of balloons I find what works best in terms of imaging the recursive pattern of nature. The MacLean in the Superverse comes to the end of its life and goes nova. Following the pattern of a hypernova the rapidly rotating core collapses in on itself giving birth to a rotating black hole within the Superverse.
Following a particle we can now trace its path as it falls into this newly born black hole within the Superverse by way of the extended Penrose Diagram for the Kerr metric. Passing through first the outer and inner event horizons it travels through the Kerr spacetime of the black hole and into the wormhole region that lies inside its volume. Remember the wormhole goes nowhere because no geodesic path escaped the collapsing core; by the Penrose Singularity Theorem. Thus its output via the inner anti-horizon and into the white hole happens within the volume of the Schwarzschild radius of the newly born rotating black hole within the Superverse. [23]
From the white hole the particle can escape either into the New Universe or the New Parallel Universe. The fact that for every white hole a pair of twin universes are born is an extremely important detail in relation to the Big Bang Hypernova Hypothesis. It is important because in looking to the pattern of a hypernova it emits a pair of gamma-ray bursts, one from each pole. In looking at CPT-Symmetry we have seen how one universe, which to us, is composed of normal matter and the other our twin universe of antimatter. We have seen how the very pattern of hypernova gives rise to the formation of these twin jets. Then by following the Penrose Diagram for the Kerr metric we are presented again with the same picture of two New Universes; the other the parallel twin.
Returning to our balloon analogy maybe blowing bubble’s by chewing gum might be a more adapt. The reason for thinking about blowing bubbles comes with thinking about the second law of thermodynamics. The balloon exists as an object before we blow into it but our universe has yet to be born; or the bubble has yet to be blown. Gum in mouth still chewing.
As a non-existent object can have no state then the number of micro-states of said non-existent object is equal to zero. By the law of entropy:
$$ S=k_b\ln\Omega\phantom{xxxxxxxxx}(10) $$
Where \(S\) is entropy, \(\Omega\) the number of micro-states and \(k_b\) is Boltzmann’s constant. The entropy of a system that is yet to be born is zero.
The hypernova of the MacLean in the Superverse gives birth to a black hole; which we consider as being one side of the coin. So on the Superverse side of the coin a black hole is born following the core-collapse of the MacLean. Then in the same location, on the other side of the coin, a white hole is born. It is at this moment when the white hole is born and begins to blow its pair of new bubble universes. These new bubble verses are causally and continuously closed vacuum spaces; as described on the Penrose Diagram.
Matter from the Superverse, such as the remainder of the exploding MacLean, then falls into the newly born black hole. As we have seen from looking at a particle falling through a rotating black hole, in the context of a Penrose Diagram, it can then be ejected into either of the two New Universes. Thus the volume of matter falling into the newly born black hole will be the matter that is ejected into either of these two New Universes that we see on the Penrose Diagram.
The matter that is forced out by the white hole into the new bubble universe will thus expand that bubble. Like blowing a bubble with gum you need to blow air out such that the pressure generated expands the elastic gum such that a bubble forms. At first a little matter hence a low number of states implying a low entropy. This entropy increases more and more as matter pours forth from the white hole which in turn expands the bubble that is the newly born universe.
Given that a black hole gives birth to a pair of new universes via the white hole then it implies that only one white hole should exist in the entire expanse of a given universe. That single white hole, the only one causally connected, to a given universe, being the very well spring of that very same universe. This is the fundamental reason why we have never observed or detected a white hole.
For all their problems, being black and compact, we have managed to detect black holes. Firstly, by detecting high energy emissions like the X-rays from Cygnus X-1. Then from observing active galaxies, or quasars, at the very edge of the visible universe. Followed by observing the fast orbit of stars at heart of our galaxy. Now, thanks to the Event Horizon Telescope, we have directly observed the supermassive black hole at the heart of the M87 galaxy. [28] [67]
However, we have never observed a white hole. We know black holes exist as strange a prediction of General Relativity that even Einstein didn’t believe in them. But yet they do! And as every physicist knows nature always loves symmetry. White holes being the symmetric opposite of a black hole thus must logically exist. So why don’t we see them in our universe? Well as a white hole gives birth to a new universe inside the volume of its parent verse then there is only ever going to be a single white hole, its source, per universe.
The white hole that gave birth to our universe lies in the heart of the void in the location where the Big Bang MacLean went nova. As I have argued this location is to be found, beyond our observable horizon, inside the Eridanus Supervoid; aka the Cold Spot on the CMB.
It is for all these aforementioned reasons that white holes are seen as an alternative explanation for the Big Bang. Thus there are a good number of papers which propose white holes as being central to the formation of our universe. Off course if the universe were born inside the confines of a black hole then surely its volume will have to fit inside its Schwarzschild radius. [33] [34] [36] [37]
But rather than our universe being born inside the volume of the black hole the Big Bang Hypernova Hypothesis looks to the structure and formation of the astrophysical jets. Astrophysical jets are in effect the most powerful particle accelerators in the universe. In order to understand the physics of the Big Bang we humans build our own particle accelerators like Fermilab and CERN’s LHC.
The collision of particles within these particle accelerators in turn produce their own “Jets”. A Jet in particle physics, resulting from the collision of particles in these accelerators, is the narrow cone of hadrons that pass through a particle detector like Atlas which was fundamental in the detection of the Higgs Boson. [59] [68]
Given that fractal geometry is the cosmological principle then self-similar patterns repeat themselves at any scale. This is called scale-invariance. In order to study the universe and the Big Bang we emulate the behaviour of nature’s own particle accelerators, astrophysical jets, in order to study the resultant particle jets. What really has peeked my interest is what Frank Wilczek’s said about finding scale-invariance, in this interview, in the fundamental equations of Quantum Chromo Dynamics. The subject of which I think will be central in a future essay. [69]
But for this work I now particularly wish to focus on the most fundamental question: What is a field? Be it gravitational or a quantum field the manifestation of our universe comes from their omnipotent presence. But what are they and where did they come from?
In the context of the Big Bang Hypernova Hypothesis I have described a concentric ringed structure the sum or which grows to becoming our universe. Specifically I see fields as having an origin story. This is particularly given focus in seeing how a hypernova explosion produces a pair of jets from which we specifically get a CPT-Symmetric structure. We live in a CPT-Symmetric universe and this is a matter of scientific fact having been the focus of thousands of experiments.
I think the vast majority of physicists think that fields themselves are the most fundamental components of nature. The idea that a field could have an origin story makes no sense and is a non question. Off course I would reply by asking why would such a person call themselves a physicist in the first place as such an attitude, to my sense of aesthetics, goes against the entire purpose and spirit of what it is to be a physicist. The never ending quest to ask that simple innocent question of “Why?” as opposed to “Shut up and calculate”. [70]
It was the idea of two jets, each travelling in polar opposite directions, as a solution to the matter/antimatter problem that gave birth to my hypothesis. It was in seeing how the formation of jets that allowed me to see how the laws of CPT-Symmetry could actually be born; as opposed to always existing. The very specific dynamics captured in my first computational model showed how such a structure could arise from the induction of a single magnet field. This in turn helped me to formulate my initial axiomatic statement which I am try to test and understand. [60]
Or rather in unpacking it I ended up using the word gravo-magnetic force. The equivalence primarily coming from Newton’s Law of Universal Gravity and Coulomb’s Law in seeing gravity as being equivalent to the electrostatic force of the Superverse. The magnetic part of “gravo-magnetic” being a force that is perpendicular to the force of gravity. Maxwell showed a magnetic wave has a perpendicular component that is an electric wave making it an electromagnetic wave. So in considering gravitational waves what is thus the perpendicular component?
Standing up, the passage of time is slower at my feet relative to the passage of time at the height of my head. This fundamentally is what Einstein’s Theory of General Relativity is saying. The force pulling me downwards towards the Earth we call gravity. The pull of gravity downwards is fundamentally coupled with this difference in the rate at which a clock ticks between my head and my feet. So in thinking about this perpendicular component to the force of gravity I am led to seeing this in the uni-directional force or arrow of time.
Time is often described as having a uni-directional arrow the past behind and the future in front. But also time, by the second law of thermodynamics, is seen as an emergent property of entropy as we continually move from a state of order to one of disorder. Relativity on the other hand looks at time as being a component of spacetime. Then in trying to describe a concentric ringed view of reality I talk about different vacuum spaces as having different and separate arrows of time. A perfect recipe for causing a whole lot of confusion.
The answer to the question, “What exactly is the arrow of time?” is probably the single hardest question to answer in all of physics. One idea of mine was thinking about how on the vacuum side of the field the arrow moves forward and inside the field the arrow moves backwards. This was the view I tried to put forward when talking about this view of what exactly a field is and what the world inside the field would be like. My initial attempt at trying to visualise a universe made up of a series of concentric rings.
This view however has been superseded in seeing how space and time swap roles when falling through the event horizon of a black hole. That is if I could magically shrink myself down so small that I could fall inside an electron or a quark what would that look like. What is the universe inside the one-electron universe?
This follows my other line of reasoning in that:
Ultimately in the Big Bang Hypernova Hypothesis I am taking the view that each concentric ring in the jet gives rise to a given field. So that one-electron universe is contained in the second concentric ring of the jet. The one-quark universe is in turn contained in the first concentric ring. And right in the middle of all things the eternal Higgs universe.
I use the word “eternal” in reference to the Higgs specifically because it has no rotation or spin hence equating it with the Schwarzschild metric. Seeing as a Schwarzschild black hole is also called a static or eternal black hole I borrow the word “eternal” in describing this non-rotating property of the Higgs particle.
So in imaging the reality inside an actual concentric field, be it an electron or quark, I imagine it being the same as inside a black hole. Both the description given in how space and time swap roles coupled with Eben Alexander’s description inside this universe gives me answer to the question. Inside the one-electron universe the roles of space and time are swapped such that space becomes time and time becomes a uni-directional dimension of space. It moves from being space-geodesic to a time-geodesic. [15]
My current attempt, in trying to imagine how a concentric ringed structured universe fits with our Standard Model of Elementary Particles superimposed upon the concentric rings identified by Roger Penrose in the cosmic microwave background radiation. The Higgs field is in the centre; the quark field the first concentric ring; the electron field the second ring; and the gravitational field upon a third ring. The force particles of the electromagnetic, weak and strong are conveyed in the vacuum spaces between the rings. [71]
The outermost ring I see as being to us the field of gravity but which to the Superverse it being equivalent to the Superverse’s electron field. Hence the realisation of my statement that gravity is equivalent to the electric field in the Superverse. That which is to us a black hole in our universe I envision as being either equivalent to a particle or an atom of matter within the Superverse.
Note that I say particle or atom within the Superverse, as opposed to fundamental particle, as in devising the origin story for supermassive black holes I see their creation as coming from the final fusion process during the core-collapse of the MacLean.
Alternatively, I could see them as being like the muon or tau particles. For reasons I will expand upon later maybe the particle of the Superverse, that is to us a black hole, gains its mass from being accelerated to relativistic speeds within the Superverse. Rather it is like the muon or tau particles in that they are second and third generations of matter, respectively, which are only found in nature coming from extremely high-energy environments such as astrophysical jets.
However a black hole manifests itself within the Superverse the critical point I am trying to communicate is that it acts in a similar manner to how an electron behaves within our own universe. As interaction with an electron releases a photon, a particle of light in our universe, so do I imagine a black hole particle acting in a similar manner in the Superverse. A particle of light in the Superverse being the force particle which is conveyed by the Superverse’s equivalent of an electromagnetic field.
This particle of light in the Superverse is not a photon. However I’d imagine it acting and behaving in a similar manner as how to a photon does in our universe in that it illuminates the Superverse. Also as our universe is continuous and causally closed such a particle has no actual physical presence or effect inside our universe. For brevity, in talking about the force particle of light in the Superverse I will simply call it a Super-photon.
The picture I have of our gravitational field is that there are two sides to the coin. Just as a black hole was one side of the coin and the white hole is the other side of the same coin so do I imagine the same for fields. On the inside of the gravitational field is our observable universe and on the other side of the gravitational field is the Superverse.
On the inside of the gravitational field the fabric of the field is continuous. Specifically the fabric or volume occupied by this field is a Lorentzian manifold of spacetime which corresponds to a solution of Einstein’s Field Equations. On the outside the gravitational field manifests itself in the Superverse through interaction with the Superverse’s electromagnetic field.
It is important to note it is not the electromagnetic field of the Superverse. As the Big Bang Hypernova Hypothesis places the origin story for our electromagnetic field in the formation of the jet then so to must it apply in the birth of the Superverse in the Super Big Bang Hypernova. Patterns repeating themselves irrespective of scale.
In the Standard Model of Particle Physics there are three generations of matter. Atoms of the periodic table are made from the first generation of matter. Up and down quarks makeup neutrons and protons of the nucleus which in turn is surrounded by orbiting electrons makes up the atom. The second generation of matter has the leptons, muon and muon neutrino, and the charm and strange quarks. The third generation of matter has the leptons, tau and tau neutrino, and the top and bottom quarks.
Rather I think the gravitational field physically manifests itself in the Superverse through interaction with the Superverse’s electromagnetic field. The more I have to come to ponder in how a given Jet-a-verse manifests itself inside its parent Jet-a-verse the more I find myself contemplating the generation of fermions. This is primarily because the only place in nature where second and third generations of particles are to be found are astrophysical jets. In particularly I wonder about the relationship between the number of concentric rings inside a given Jet-a-verse and the number of possible generations. Why there are only three generations of particles is one the great unsolved mysteries of physics.
Gravitational waves, as predicted by General Relativity, are disturbances in the curvature of spacetime, generated by accelerated masses, that propagate as waves outwards from their source at the speed of light. The collision and merger of two black holes into becoming a single black hole is such an event that generates these gravitational waves. The two LIGO observatories famously detected and proved the existence of gravitational waves in 2015 from such a black hole merger. [72]
In thinking about the gravitational field and its waves we know that from inside our universe we detect these waves from the vibration in the metric of spacetime. This is an effect of General Relativity.
But on the other side of the gravitational field in the Superverse I imagine its manifestation as being a quantum effect. So in the Superverse we see two particles merge into a single particle which in turn releases a Super-photon. This Super-photon will then start its journey travelling across the Superverse until it reaches the eye of an observer living within the Superverse. Thus an observer in the Superverse can have knowledge of the black hole merger event that we saw happening inside our own universe.
With this duel nature of the gravitational field described I can now give description of how I view a field whose particle has both mass and charge. Specifically in viewing the gravitational field as a concentric ring so too are the electron and quark fields also concentric rings. More generally, it is any concentric ring shaped field be it belonging to our universe or the Superverse or any other such Jet-a-verses.
The origin of story of a field, in the context of the Big Bang Hypernova Hypothesis, comes in the unfolding of a given jet into a series of concentric ringed structures as captured in my first computational model. Each of these jets shares the same axis of rotation, which for us is around the central Higgs field, that is the middle point of the jet. The concentric field belonging to a given Jet-a-verse thus originates from the white hole that gave birth to the given Jet-a-verse.
Also another important point is to remember that there are two jets each travelling in polar opposite directions from the other. The axis of rotation of the MacLean that went hypernova is imparted to the rotation of the newly born black hole in the Superverse. This then defines the direction of travel each of these two jets as they start their journey across the expanse of the Superverse. It is important firstly because it first explains how our CPT-Symmetric universe came into being. Secondly, by the extended Penrose Diagram of a Kerr black hole the white hole opens out into two New Universes. [2]
The idea that two universes arose as a result of the Big Bang is certainly not new. Andrei Sakharov, a Russian nuclear physicist, developed a 2D-didactic cosmological model in considering both baryon asymmetry and CPT-symmetry. More recently Jean-Pierre Petit developed his Janus Cosmological Model based upon Sakharov’s work. Additionally there is Julian Barbour’s work which shows a gravitation origin to the arrow of time. This produces the result that two universes emerge from the same point, called the Janus Point, whose two directional arrows of time are opposite to each other. [73] [74] [75] [76] [77] [78]
Janus being the name of the two headed Roman god of gateways. Though personally I’ve got to give it to the Roman pantheon but it takes a twin to understand such Twin cosmological models as Apollo draws in closing upon His prey. Perfectly lined up for the greatest kill in all of cosmology. [79]
As we described with the gravitational field a concentric ringed field has two sides to it, an inner and outer surface. Adjacent to each of the surfaces is a vacuum space. Using our analogy of imaging a field as a balloon; the inner vacuum space is the air inside the balloon and the outer vacuum space is the air surrounding the outside of the balloon.
The difference between being inside a vacuum or a field comes down to the configurational state of spacetime; be it a space-geodesic or a time-geodesic. In a field with no rotation we describe it using a solution similar to the Schwarzschild metric; as in the case of the Higgs Field which has no spin. For a concentric field we use a Kerr metric in describing the geometry of spacetime. In a vacuum or a wormhole the configuration of spacetime is a space-geodesic with 3 spatial dimensions and a single temporal dimension. Inside a field, between horizons, space becomes time giving 3 temporal dimensions with a single spatial dimension; a time-geodesic.
As a note, in describing fields I am using the word “surface”. This is purely for the sake of simplicity and understandability. A concentric field, as well as the fields contained within it, can be said to be omnipresent within the volume occupied by the outer vacuum. The Higgs field and electron field being omnipresent within our universe as both originated from the same white hole. However the Higgs field and electron field are not present or have physical meaning in the vacuum of the Superverse. The fields in the Superverse have meaning coming from the white hole that gave birth to the Superverse.
In saying this I have to reflect upon my axiomatic statement from earlier that says “Gravity is equivalent to the electromagnetic force, but on the next scale up in Superverse”. In light of what we have just talked about our gravitational field was born from the Big Bang white hole and is not omnipresent in the Superverse. However my computational model shows that the concentric ringed jet is shaped by the electromagnetic force of the Superverse. So in saying this let us define the fields of the Superverse such that we can resolve this conflict in logic.
The equivalent of the electron field of the Superverse we now call the Super-electron field. Also the equivalent of the gravitational field of the Superverse we now call the Super-gravitational field. Both of these concentric ringed fields of the Superverse originate from the white hole that gave birth to the Superverse’s Jet-a-verse. The force mediated by the Super-photon spans the vacuum of the Superverse. In a nutshell, we take an exact copy of the concentric ringed structure we used in describing our universe and scale it up such that we can define the structure of the Superverse. We do this by the law of self-similar patterns and scale-invariance.
So in giving birth to our Jet-a-verse the MacLean in the Superverse goes nova. The core-collapse gives birth to a black hole in the Superverse which in turn feeds. In effect the fabric of the Super-electron field surrounding the feeding black hole is sucked into it. Or rather the rotating black hole becomes charged into becoming a Kerr-Newman black hole.
What I think happens is that the Super-electron field is effectively transformed by the Kerr-Newman black hole such that when it is ejected, via the pair of jets, it is now become the gravitational field of our Jet-a-verse. Effectively, that is to say our gravitational field is derived from the Super-electron field by the black hole born in the Big Bang Hypernova.
The Super-electron field of the Superverse is consumed by the Super-black hole born in the Big Bang Hypernova. Falling through the black hole, shown as the glass sphere in the animation, the field of the Superverse is ejected into our universe via the jet such that it becomes our electron field. So we can say our electron field is derived from the Super-electron field. That is, the Super-electron field is transformed into our electron field by the Super-black hole born in the Big Bang Hypernova.
The manifestation of the gravitational field in the Superverse, being derived from the Super-electron field, thus interacts as part of this Super-electron field. Interaction upon this derived Super-electron field with the vacuum of the Superverse produces Super-photons which light the Superverse. The particle representation of this derived Super-electron field, which is to us the gravitational field, being equivalent to a second or third generation particle of the Super-electron field. That is, the particles are Super-tau or Super-muon particles.
I think that is the best way I can currently describe it for now as in this work we have really only so far considered rotation via the Kerr metric. In future work we’ll look at describing charge particularly in the context of Reissner–Nordström black holes such that we can explore and further unpack the origin story of fields. For the moment let us return to trying to describe the structure and behaviour of a field.
The inner surface is continuous and causally closed and is shaped from the inside by physical matter with a positive mass-energy density. Using our analogy of being inside a balloon; the mass of a physical object, like a metal sphere, will deform the elastic surface of the balloon in an outwards direction. The greater the mass-energy density of a given object the greater the deformation of the balloon’s elastic surface. At a critical limit if the mass-energy density of a physical object becomes so concentrated, in a small enough volume, then it falls into the inside surface of the field at which point it becomes a particle upon that field.
The deformation of the gravitational field by a mass inside our universe deforms the field outwards. Vice versa, the deformation of the gravitational field inwards comes from mass outside our universe. That is from an object that has mass that exists in the Superverse. This follows how in my original thesis I describe the formation of the Bootes Supervoid.
The Earth deforms the fabric of spacetime enough that it has an escape velocity of 11.2km/s. The Sun being more massive than the Earth deforms the fabric of spacetime even further. Then moving right up the mass-energy density scale we have White Dwarfs and Neutron Stars. But for a black hole the mass-energy density is so great that to us it collapses infinitely in on itself. The critical limit is such that the escape velocity at the event horizon is equal to the speed at which information can travel across the fabric of the given field. In the case of our gravitational field inside our universe this is equal to 299,792,458 m/s which is the speed of light.
The outer surface forms the physical basis of all things in the outer vacuum space. Well the particles inside the field form the outer most physical layer whose summation forms the reality of the outer vacuum space. Quarks encased by the electron’s concentric field form protons and neutrons. For us the electron concentric field forms the outer layer and thus the nucleus of atoms are encased inside the orbiting electrons.
Given a critical limit and its relationship to the speed of information transference on a given field I feel there is very important relationship between this and the mass-energy of a given particle. All electrons have mass-energy density of \(0.511MeV/c^2\), up quark has \(2.2MeV/c^2\) and down quark has \(4.7MeV/c^2\). They are all the same as they all arise from the same concentric fields that have existed since the time of the Big Bang.
However this relationship with the outer surface of a field works in a quantised and integer based manner; hence quantum mechanics. I am pretty sure that someone with a far deeper knowledge of quantum field theory and its mathematics could give a much more accurate and better description. But as a simple analogy this vision of a balloon works particularly in taking about elastic, pressure and tension; such as when talking about Hubble tension. [80]
Each particle upon the field acts as a vortex into the field. On the inner surface a black hole is effectively a vortex into that field. The analog models used to understand black holes are literal whirlpool vortices. The same I believe is possibly also the case for particles on the outer surface of field. The primary reason for saying this comes particularly from superfluids and quantum vortices. Though the ability to effect the outer field by temporally extending the inner field is where the real party is at in talking about Cooper-pair mass anomaly. [40] [81] [82] [83] [84]
Another reason comes from Leonard Susskind and Juan Maldacena’s ER=EPR conjecture. As a Kerr black hole is causally connect to a white hole via a wormhole so too is it for entangled particles. That is a particle which exists in a state of superposition in more than one location is internally connected via wormholes within that field. [85]
Or in plain English, these are the keys to anti-gravity, warp drive and full interstellar travel technologies. So if you dream of such things then, in my humble opinion, this is where we need to focus our full attention.
Having now given description of a concentric field let us now discuss those force particles that traverse the vacuum space. A force particle arising from an event on the inner field of a vacuum traverses the spatial dimensions of said vacuum. The rate at which a particle can traverse the vacuum is determined by the outer field. So a photon arising from the electromagnetic field travels at the speed of light which is determined by the gravitational field.
A particle with charge, like the electron, is in orbit around the central Higgs Field. The electron neutrino has no charge and can be viewed as a particle upon the electron field. However the neutrino is not orbiting the central Higgs Field. In effect an electron neutrino is an electron that is no longer in orbit around the universe’s central axis of rotation.
A particle with charge can be said to be rotating around the central axis. This is a direct interpretation from looking at CPT-Symmetry as I attributed charge with this orbital rotation around the central axis. The spin I picture more as the orbital rotation of a spherical particle. But when spin is a half it belongs to concentric field and when equal to one it is a force particle that traverses its given vacuum.
Then we have neutrinos which have exactly the same half spin but no charge. As there is no charge it means that the particle is no longer in orbit around a central axis of rotation. Or rather it is Higgs invariant as it no longer orbits that field. An electron with charge, based on my interpretation of CPT-Symmetry, is in orbit around this central axis. So to have zero charge means it must not be in orbit because the electron has been effectively separated from its actual electron field by a high-energy event such as nuclear fusion.
Looking at the structure of our Jet-a-verse we start from the centre in building up our description of a concentric universe. In doing so I wish to finally return to answering the question; What is the arrow of time in the context of the Big Bang Hypernova Hypothesis?
In talking about time and the arrow of time I need to make two classifications. The first comes in thinking about fluid flow in a volume of water. Mathematically to every point in the continuous volume of water we assign a vector such that it is described as a continuous vector field. The direction in which the water flows is the direction in which the universe is moving. In cosmology, the universe can be described as a fluid because the equations of perfect fluid flow are an exact solution of Einstein’s field equations of General Relativity. [86]
In the centre is the central Higgs field with no spin and no charge. The Higgs field is the very axis of rotation around which the entire universe rotates. When talking about the universe as a whole the physical manifestation of this vector field describing the motion of the universe is the Higgs field itself.
More than that it acts as the very heartbeat which hammers out the beat from which causality flows. In order to hear this heartbeat we require something that has an extremely high mass-energy density coupled with conditions such that all other noise is removed. A neutron star in space is one such example. Another example being super-cooled, to remove noise, heavy atoms such as Caesium. Both examples are to us the most accurate clocks.
At the centre of all things is this heart beat that both points the direction of travel but also in turn provides the metronome from which causality flows; the Higgs Field.
The second classification is the emergent property of causality within a vacuum space. At the quantum level, in a given vacuum space, we measure entropy. This statistical property forms shape the more we zoom out. In a computational model, such as a Lattice-Boltzmann model, statistics are used in order to plot the overall distribution of particle movement. As an example, if you have a Nvidia graphics card there is this shallow-water simulation of raindrops which I developed in the days before the Big Bang Hypernova Hypothesis came to me.
This second classification of the unidirectional arrow of time is an emergent property of a given vacuum space as it moves from order to disorder as entropy increases. This arrow of time is the second law of thermodynamics and applies only to a given vacuum space.
Let us now look at the structure of the full jet in cross-section as we move from the centre outwards. As already described, the Higgs field is at the centre of all things in our universe as it points the way to the rhythm of its beat.

Left, the concentric ringed model of elementary particles for the Big Bang Hypernova Hypothesis. Right, the actual standard model of particle physics. The first vacuum space, the strong vacuum space, lies between the Higgs and Quark fields where force is conveyed by the gluon. The second vacuum space, the weak vacuum space, lies between the Quark and Electron fields where force is conveyed by both the Z and W-Bosons. The third vacuum space, the photon vacuum space, lies between the Electron and Gravitational fields where force is conveyed by the the photon.
Moving outwards we encounter the first vacuum space where the gluon is the particle of light. Here in this the strong vacuum space a forward unidirectional arrow of time emerges from the quantum field of the Higgs.
Next we encounter the first concentric field which is responsible for the up and down quarks. It is the physical field for all quarks but as we discussed the other generation of quarks arise from the fields of recursive sub-Jet-a-verses. Collectively the quarks physical presence comes in the surrounding outer vacuum as we next encounter the weak vacuum space. Both the Z and W-Bosons are the force particles inside this space.
Again in this vacuum space an arrow of time emerges. The arrow of time inside the weak vacuum space is independent of the photon vacuum space’s arrow of time. Information flows from the centre out. This view comes particularly in understanding why radioactive decay, as mediated by the weak force, is invariant to the arrow of time we experience; being made up of atoms.
Between the weak and the photon vacuum spaces is the electron field. This in turn encloses the quark field inside the proton and neutron of the atomic nucleus. The volume between the nucleus and the orbital electrons is the weak vacuum space. Thus when we come to the photon vacuum space yet again another arrow of time emerges. In fact, it is the single most important arrow of time for us as it is the one we experience in life.
After the photon vacuum space there is finally the gravitational field and beyond that the vacuum of the Superverse. So on our side of the gravitational field it is continuous and causally closed. A black hole is a particle upon that field. On the other side of the gravitational field inside the Superverse that which is to us a black hole manifests itself as a particle, such as the Super-tau or Super-muon, upon a quantum field inside the Superverse.
In order to talk properly in describing the structure and shape of the Superverse I find I need to create the right nomenclature and definitions in order to even talk about them. My current attempt lacks flexibility in simply prefixing everything with the word “Super”. But even without that I would be constantly saying things like “equivalent of the Superverse’s electromagnetic force” or the “Superverse’s gravitational field”, or “black hole born into and belonging to the Superverse”; leading us into a linguistic quagmire full of confusion.
To this end I will use the notation S(n) as a prefix in reference to a field, particle or force belonging to a given Jet-a-verse. The n is an integer number that counts the level of recursion with zero being in reference to our own Jet-a-verse. So in saying the S(0) Jet-a-verse I am specifically making reference to our own universe. The S(1) Jet-a-verse is what we have been calling, up until now, the Superverse. The S(2) Jet-a-verse is then the Super-superverse.
So our universe the S(0) Jet-a-verse is contained inside the volume of the S(1) Jet-a-verse. In turn the S(1) Jet-a-verse is contained inside the volume of the S(2) Jet-a-verse; remembering our analogy of balloons.
Blowing air into a green balloon inflates it. As it inflates with air the volume of the green balloon grows and expands. By falling through the nozzle of the green balloon we come to be inside the volume of the green balloon. Now air from inside the green balloon inflates a red balloon. As the red balloon inflates with air its volume grows such that it occupies a subset of the volume inside the green balloon. By falling through the nozzle of the red balloon we come to be inside its volume. Repeating the process, air from inside the red balloon inflates a blue balloon. So the volume occupied by the inflated blue balloon is a subset of the volume inside the red balloon. Recursively we can continue this cycle of falling inside the volume of subsequent balloons.
As we just described for our S(0) Jet-a-verse it is composed of a series of three concentric ringed fields all of which rotate around a central Higgs’s field. By the law of scale invariance we infer the exact same pattern to the Superverse; or rather the S(1) Jet-a-verse. Hence we have
S(1) Higgs Field - The central field of the Superverse, being equivalent to our Higgs field, around which all the concentric fields of the Superverse rotate. The particle representation of this field is an S(1) Higgs particle.
S(1) Quark Field - The first concentric field of the Superverse, being equivalent to our quark field. The particle representation of this field is an S(1) Quark.
S(1) Electron Field - The second concentric field of the Superverse, being equivalent to our electron field. The particle representation of this field is an S(1) Electron.
S(1) Gravitational Field - The third concentric field of the Superverse, being equivalent to our gravitational field. The particle representation of this field only makes sense in the S(2) Jet-a-verse.
The origin story we have given to the S(0) fields inside our universe tell us that they arose from the concentric circular structure of the jet arising from the Big Bang Hypernova. We have seen how, like blowing up a bubble, a pair of new universes can be born via a white hole coming from the birth of a rotating black hole. The structure imparted to these new born twin universes comes from the concentric circular structure of the jet.
In talking about black holes and white holes we define:
S(0) Black Hole - A black hole inside our universe. The S(0) black hole is upon the S(0) gravitational field.
S(1) Black Hole - A black hole inside the Superverse like the ones born from the core collapse of a MacLean going hypernova. The S(1) black hole is upon the S(1) gravitational field.
S(0) White Hole - The white hole which is both causally connected and born when a S(1) black hole is born. We say that the S(0) white hole gives birth to a twin pair of S(0) Jet-a-verses.
S(1) White Hole - The white hole which is both causally connected and born when a S(2) black hole is born in the S(2) Jet-a-verse.
So we can say now, that a pair of S(1) Jet-a-verses were born by the S(1) white hole which in turn was born following the core-collapse of a S(2) MacLean into a S(2) black hole. In turn, the Big Bang Hypernova gave birth to an S(1) black hole which in turn gave birth to a S(0) white hole and subsequently a pair of S(0) Jet-a-verses; one of which is the universe we live in today.
Lastly in giving description to the S(1) Jet-a-verse, the Superverse, we need to define its vacuum spaces between each of the concentric fields. Following the same concentric description given to our S(0) Jet-a-verse:
S(1) strong vacuum space - The vacuum space between the S(1) Higgs field and the S(1) quark field. The force boson is the S(1) gluon which conducts the S(1) strong nuclear force.
S(1) weak vacuum space - The vacuum space between the S(1) quark field and the S(1) electron field. The force bosons are the S(1) Z and W-Bosons which conducts the S(1) weak nuclear force.
S(1) photon vacuum space - The vacuum space between the S(1) electron field and the S(1) gravitational field. The force boson is the S(1) photon which conducts the S(1) electro-magnetic force.
This new framework of describing S(n) Jet-a-verses follows directly from the assumption that fractal geometry is the cosmological principle. The Superverse must follow the laws of physics as we know them inside our universe because of the existence of starlike objects that I called a MacLean. That is star’s in the S(1) Jet-a-verse are almost exactly like stars in our universe following a life cycle of fusion and death by core-collapse.
Rather it is to say the “fine-tuned constants” of our universe are directly inherited from our parent S(1) Jet-a-verse. The S(1) black hole / S(0) white hole act as a scale transformer from the larger reality of the Superverse in giving birth to our universe. Just like a scaled model train set is a mirror reflection of a real railway system; so is our universe a mirror reflection of its parent Superverse. This scale transformation being seen in how a given metric is reduced to zero at the event horizons within a rotating black hole. This idea of scale transformation is what is directly reflected, as discussed, in the bases of those artworks which inspired this piece.

Upon this rock He did make his mark... only to have a totally insane lunatic like me to come along 2000 years later to blatantly copy it as it makes the perfect logo for my website. Though in designing my logo, on the right, I left out the steps as I had not seen their true value. I love my logo as I can show the beauty and simplicity of my hypothesis in describing how a natural sequence of events gave birth to our universe. No need to invoke a higher power. On the other hand it is one of the best doodle’s of a penis from antiquity as if it was some kind of F-you to His future executioner. Those spirals, the hairy bollocks, we’ll caress later in a live fire practical demonstration of naked power. What is it with creation myths and dicks? Birth I guess. I guess He must have just heard the tale of creation of Atum while drawing this. Definitely not thinking about His grandfather Uranus as the logo has “hairy bollocks”. I here tales of Saturn and a scythe.
Now that we have a full description of the Superverse how exactly does our S(0) gravitational field actually manifest itself in the S(1) Jet-a-verse?
The S(0) gravitational field originates at the S(1) black hole that birthed it. The S(1) electromagnetic field originates at the S(2) black hole that birthed it. A S(0) black hole we view as a particle upon the S(0) gravitational field. So how does this particle manifest itself inside the Superverse?
Well the main force that shaped the S(0) fields is the S(1) electromagnetic field following the results of my first computational model. As the shape of the jet was given form following magnetic induction in the computational model I infer this to the Big Bang Hypernova in saying that the S(1) electromagnetic field shaped the structure of our jet.
Or as we discussed earlier, the S(0) gravitational field is derived from the S(1) electron field. The input to the S(1) black hole being the S(1) electron field which is then scale transformed into the output S(0) gravitational field via the associated S(0) white hole.
So as the S(0) gravitational field is shaped by the S(1) electromagnetic field then its manifestation inside the Superverse would be via the S(1) electromagnetic field. This actual manifestation I feel is given form, as we discussed earlier, in considering that there are three generations of particles within the standard model of physics. Or rather the manifestation of a S(0) black hole in the Superverse would be equivalent to an S(1) muon particle. Again the primary reason for thinking this comes from considering that the natural source of second and third generation particles inside our universe are coming from astrophysical jets.
One immediate thing stands out is in describing supermassive black holes as being the heavy atoms of the Superverse. But on the other hand I describe their particle representation as being a single fundamental particle like the S(1) muon. Maybe in fact all the particles both the S(1) electrons and the S(1) quarks that make up this heavy atom of the S(1) Jet-a-verse become S(1) muons, S(1) charm and S(1) strange particles. But to us it is a supermassive black hole. Certainly a black hole is like an atom in regards to the majority of the mass being concentrated at a single central point, be it the nucleus or singularity. I make the comparison by the law of self-similarity and scale invariance.
We now come to considering how a black hole inside our universe would give birth to a pair of sub-verses inside the volume of our universe. As the Big Bang Hypernova Hypothesis specifically describes how a S(1) black hole being born gives birth to our universe via its S(0) white hole; then by the same logic of recursion so to must sub-verses be born inside our universe. Hence it gives us a way to test the validity of the Big Bang Hypernova Hypothesis.
In describing a Jet-a-verse inside our own S(0) Jet-a-verse we use the word subverse to describe it as it is a subset of the S(0) Jet-a-verse. Using our new notation we can also call this Jet-a-verse inside our own universe a S(-1) Jet-a-verse where a negative number means it is actually inside the volume of our own universe.
A S(0) black hole being born in our universe will lead to a S(-1) white hole being born. This new S(-1) white hole gives birth to a pair of new S(-1) Jet-a-verses. These S(-1) Jet-a-verses are shaped are structured by the forces that shape the pair of astrophysical jets emitted from this newly born S(0) black hole. Like a pair of bubbles being inflated from the poles of the S(0) black hole these new continuously and causally closed S(-1) Jet-a-verses grow. Thus a pair of balloon shaped volumes are inflated from the polar regions of the given S(0) black hole by the material falling into it.
Material falling into the S(0) black hole will be ejected into the pair of S(-1) Jet-a-verses. As long as material is falling inside the S(0) black hole then we can assume that a pair of astrophysical jets will also be ejecting material that is itself entangled with this new pair of S(-1) Jet-a-verses. When material stops falling in the pair of S(-1) Jet-a-verses will remain as inflated bubbles occupying the polar regions of the S(0) black hole.
Now in the Big Bang Hypernova Hypothesis I described the origin story of supermassive black holes as being formed following the fusion of heavier and heavier elements in the Superverse. Applying the same logic an atom of an element in this our S(0) Jet-a-verse will become equivalent to an S(-1) black hole in the S(-1) Jet-a-verse. These black holes will be present on the S(-1) gravitational field but, based on our discussion of second and third generation particles earlier, it would be equivalent to a S(0) muon or S(0) tau particle or simply a muon or tau.

Viewing the muon as being a particle associated with a S(-1) Jet-a-verse then one might be tempted to say that we require “New Physics” to describe it. Oh wait, hang on! Breaking news just in Fermilab have just unveiled the results of the Muon g-2 experiment with them saying “finds strong evidence for new physics”. What a happy coincidence in time that helps make my case. Just like the time last year we accidentally lost an entire star after writing about the exact subject. Like the reality of the muon yet again I find reality has gone a bit of axis, wobble wobble. Time to stack the plates or the rotors, being a first for humanity. [87] [88] [89] [90]
Like S(0) black holes in our universe these S(-1) black holes can also collide and merge inside the volume of the S(-1) Jet-a-verse. As the S(-1) gravitational field is equivalent, or rather derived from, our own S(0) electron field then this black hole merger in the S(-1) Jet-a-verse would create a high energy S(0) photon upon the S(0) electromagnetic field inside our own S(0) Jet-a-verse.
As the S(-1) Jet-a-verse is a scaled down version of our own S(0) Jet-a-verse I would imagine the passage of time inside the S(-1) Jet-a-verse to be far faster than our own. Meaning that if we consider the heat death of our universe as being on the scale of hundred of trillions of years then such a scale for an S(-1) Jet-a-verse is vastly shorter. And the scale of hundred of trillions of years inside our S(0) Jet-a-verse could be the equivalent of a million years in the Superverse. Though I have funny suspicion that four billion years, the age of the Earth, equates to about a single week in the Superverse.
The point about the rate of time is that the number of S(-1) black hole collision events would be numerous enough such that the bubble of the S(-1) Jet-a-verse would effectively cause it to glow. Being high energy events, thus high energy photons, the expected radiation glow would be towards the X-Ray end of the electromagnetic spectrum.
NASA’s Fermi Gamma-ray Space Telescope, which has been operating since 2008, has identified an entirely new structure to our own Milky Way Galaxy called Fermi Bubbles. Originating from the centre of our galaxy these twin bubble structures only appear in the X-Ray and Gamma-Ray end of the spectrum. [4] [5]
Spanning 50,000 light years in length these twin pair of Fermi Bubbles occupy the polar regions, above and below, the intergalactic plane of the Milky Way galaxy. We see twin pairs of astrophysical jets coming from active galaxies whose supermassive black hole is feeding. Then because of this behaviour the formation of these Fermi Bubbles has been linked to our own supermassive black hole Sagittarius-A* in the heart of our Milky Way galaxy. This particular study looks at the formation of Fermi Bubbles as being the shock front coming from recent jet formation some 5 million years ago. [91] [92]

Fermi Bubbles, visible in the X-Ray spectrum, are observed extending from the centre of our spiral Milky Way galaxy. Spanning about 50,000 light years in length these newly discovered structures of our own galaxy shows the invisible interaction between an existing pair of S(-1) Jet-a-verses and our own universe. All this follows from seeing a rotating black hole as a scale transformer through the lens of fractal recursion.
In the context of the Big Bang Hypernova Hypothesis these Fermi Bubbles are the radiation glow of the S(-1) Jet-a-verses originating from the Sagittarius-A* supermassive black hole. Coming from events on the S(-1) gravitational field we see these high energy events upon our S(0) electromagnetic field. So in effect, the matter that fell into the Sagittarius-A* black hole was ejected into the associated twin pair of S(-1) Jet-a-verses. We can know information about this matter that has previously fallen into the Sagittarius-A* black hole as it is encoded in the light from such high energy events on the S(-1) gravitational field.
This in effect is how the Big Bang Hypernova Hypothesis looks to answers the Black Hole Information Paradox. That and it also provides a very simple explanation to why Fermi Bubbles exist and why we are able to observe them.
But what happens when the S(-1) Jet-a-verses cool down and effectively become as our universe is expected to become a hundred trillion years from now. Namely, the heat death of the S(-1) Jet-a-verse would see a verse whose only remaining matter now resides in the heart of its S(-1) black holes. The S(-1) Jet-a-verse has expanded so much that black hole collisions are a very rare thing. In effect, all the matter in the S(-1) Jet-a-verse is locked away inside its own continuously and casually closed manifold.
Although the S(-1) Jet-a-verse no longer emits radiation into our universe the mass locked inside it still remains contained inside the volume of our S(0) Jet-a-verse’s manifold. It no longer has a particle representation; the muon and tau particles in the actual astrophysical jet having decayed long ago. But in turn maybe the decay of the muon and tau particles would be equivalent to the evaporation of the S(-1) black hole. But in effect, until the S(-1) black holes evaporate, it is an enclosed manifold of matter with mass inside the volume of our own universe. It may not have a particle representation but its effects can still be felt in terms of bending the fabric of spacetime inside our own universe.
Or to put it another way; this is how the Big Bang Hypernova Hypothesis accounts for the existence and origin of dark matter and why after nearly half-a-century later we have found no evidence of an actual dark matter particle. But at the same time it also accounts for why we can observe its effect in the rotation of galaxies and via gravitational lensing.
This is the CDM of the Big Bang Hypernova Hypothesis model; the cold dark matter.
The revelation that universes are each contained within the volume and confines of its parent verse is one that leaves me speechless. No words are adequate to describe their wonder and beauty. The fractal Mandelbrot set is but a pale shadow of the true cosmological fractal. And all this behaviour arises from understanding that the true nature of black holes is to act as a scale transformer; the kernel of recursion.
But let us go further in realising that recursion can occur in the S(-1) Jet-a-verse. This gives rise to a S(-2) Jet-a-verse and that can contain a S(-3) Jet-a-verse. Ultimately, I believe this pattern of recursion leads us to the birth of actual particles upon the fields of the unfolding jet. Or rather, the complexity that arises from this leads to quantum particles inside our S(0) Jet-a-verse which are intimately tied to S(0) black holes.
This vision is probably best given clarity in physics in thinking about the Holographic Principle. What has really peaked my interest was this interview with physicist Nassim Haramein in which he describes how he managed to calculate the theoretical s ize of a holographic proton. His theoretical prediction matches the experimentally measured size of the proton. Prior to this the theoretical size of a proton was off by about a 10% margin meaning something was wrong with the theory. This is yet another area where I am going to concentrate my effort in order to understand this. [93] [94] [95]
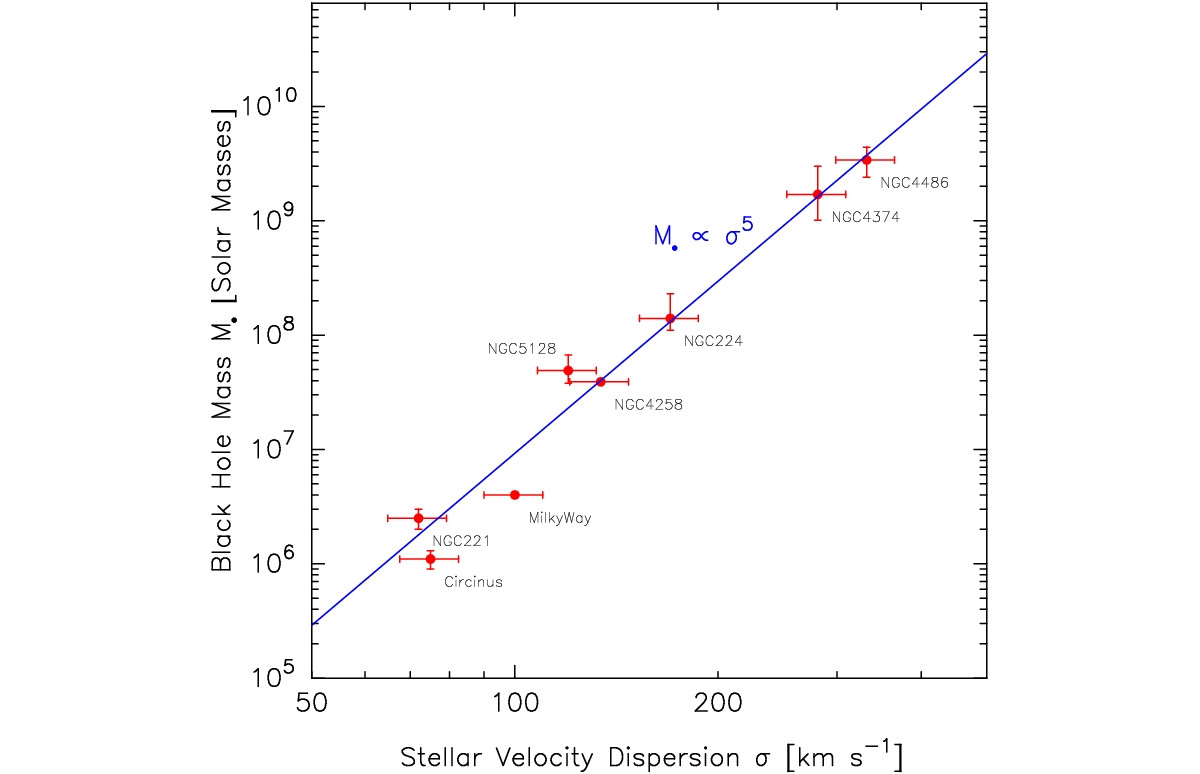
Black-hole mass plotted against velocity dispersion of stars in a galaxy bulge. Points are labelled by galaxy name; all points in this diagram are for galaxies that have a clear, Keplerian rise in velocity near the center, indicative of the presence of a central mass. The M–σ relation is shown in blue.
Another important piece of evidence in showing the very intermittent connection between a galaxy and its supermassive black hole comes in the clear linear relationship between the rotational velocity of galaxy and the mass of its supermassive black hole. Or more specifically, the M-sigma relationship plots a linear relationship between the velocity distribution of the galactic bulge and the mass of a galaxy’s supermassive black hole. [96]
Now everything I have presented and talked about so far is all building from a single key assumption that the universe has rotation at the largest scale. If there is no rotation of the universe at the largest scale then this implies the Big Bang originated from a point singularity. As we saw, the Lambda-CDM model is built upon this one single assumption. My argument replaces this gravitational singularity with the ringularity of the Kerr metric allowing us to envision the white hole as the Lambda of the Big Bang Hypernova Hypothesis model.
So what is the evidence that at the largest scale the universe is actually rotating at the time of the Big Bang event?
The answer it turns out looks like it is reflected in the quadrupole map of the Comic Microwave Background Radiation. In order to talk about the quadrupole map we need to talk first about multipole expansion.
The Cosmic Microwave Background Radiation in effect is the light energy, now red-shifted to the microwave end of the electromagnetic spectrum, that has been traversing the universe since the time shortly after the Big Bang event itself. The photons of this light energy we measure, in experiments like WMAP and Planck, coming from every heavenly direction. In measuring these photons we also measure the direction in which a photon came from. Thus to each sampled photon a set of spherical coordinates, the polar and azimuth angle, is assigned in recording from which direction of the observable horizon it came from.
A multipole expansion is a function written as a mathematical series, most commonly as a sum of spherical harmonics, where that function is dependent on angles. It is employed as an analysis tool where the collected data can be mapped onto a sphere. In the case of the CMB this sphere we describe as being our observable horizon.
The maps produced from multipole expansion are dependent upon the number of sums in a given series. The greater the number of sums, used in expressing the function, the higher the resultant resolution of the map as finer angular features are revealed. However, the higher the resolution the greater the number of data samples required.
This resolution of the multipole maps is expressed in terms of progressively finer angular features or moments. The first term, in the summation, is called the monopole moment. The second term is called the dipole moment; the third the quadrupole moment; the fourth the octopole moment; and so on. A multipole moment usually involves powers and is expressed in terms of \(2^n\) where \(n\) is a positive integer.
The function used is for calculating the blackbody temperature radiation given the sampled photons’ energy. Hence the maps produced of the CMB are expressed as temperature maps; nearly always expressed in units of Kelvin. The established view being that the hotter a region is the higher the mass-energy density in that region of the universe.
As the universe looks more or less the same in every direction, observing galaxies whose laws of physics are the same as ours, the expected conditions that gave rise to this sameness was exactly that; specifically all the same. This is the cosmological principle that our universe is, on the largest scale, homogenous and isotropic in full effect for the aforementioned reason. Hence astronomers expected that the CMB sky should be exactly the same all over. This was confirmed to be true, at first, from the earlier experiments to measure the CMB which found near uniformity throughout the microwave sky.
With better experiments such as COBE small variations in the temperature were measured. This variation first showed itself in the dipole map of the CMB. This variation was determined to be a Doppler shift arising from our Solar System’s direction and speed of travel relative to the rest of the universe. [97] [98]
Now at this point I wish to point back to my earlier discussion in describing how I believe that central to all things in the universe there is a direction of flow. That being the Higgs field is at the very centre of our concentric ringed universe and the direction of flow being the physical manifestation of this jet. In terms of solutions of spacetime we can describe it as a perfect fluid seeing as the equations of a perfect fluid are an exact solution to Einstein’s field equations. [86]
Here this direction, with respect to the underlying anisotropy in the dipole map, was used from the moment it was discovered in order to correct the subsequent maps of the CMB. Thus all subsequent maps produced of the CMB had to account for this Doppler shift. This Doppler shift in the resultant CMB was because our solar system is moving 370km/s relative to the rest of the universe.
The quadrupole map from the Tegmark et al. (2003) cleaned map, presented in Galactic coordinates, after correcting for the kinetic quadrupole. The solid line is the ecliptic plane and the dashed line is the supergalactic plane. The directions of the equinoxes (EQX), dipole due to our motion through the Universe, north and south ecliptic poles (NEP and SEP) and north and south supergalactic poles (NSGP and SSGP) are shown. The multipole vectors are plotted as the solid red symbols for each map, ILC (circles), TOH (diamonds), and LILC (squares). The open symbols of the same shapes are for the normal vector for each map. The dotted line is the great circle connecting the two multipole vectors for this map. The minimum and maximum temperature locations in this multipole are shown as the white stars. The direction that maximises the angular momentum dispersion of any of the maps coincides with the respective normal vector as discussed in the text. [99] [100]
The real problem about the large scale anisotropy came in the production of the quadrupole and octopole maps of the CMB. Specifically in the quadrupole map there are four large scale lobes. These four lobes have a temperature variation of about from the average with two hot interleaved with two cold lobes. More curious is how these lobes are aligned with the ecliptic plane of our own Solar System. The octopole map shows us six lobes, three cold interleaved with three hot, again unusually aligned with our ecliptic plane. [99]
The octopole map from the Tegmark et al. (2003) cleaned map, presented in Galactic coordinates. The solid line is the ecliptic plane and the dashed line is the supergalactic plane. The directions of the equinoxes (EQX), dipole due to our motion through the Universe, north and south ecliptic poles (NEP and SEP) and north and south supergalactic poles (NSGP and SSGP) are shown. The multipole vectors are the solid magenta symbols for each map, ILC (circles), TOH (diamonds), and LILC (squares). The open symbols of the same shapes are for the normal vectors for each map. The dotted lines are the great circles connecting each pair of multipole vectors for this map. The light gray stars are particular sums of the multipole vectors which are very close to the temperature minima and maxima of the multipole. The solid black star shows the direction of the vector that appears in thetrace of the octopole,T3(29), of the TOH map. The solid magenta star is the direction to the maximum angular momentum dispersion for the octopole, again for the TOH map. [99] [100]
To say these large scale anisotropies has been problematic to our understanding of cosmology would be to put it very mildly. Certainly a very large effort has been put into both the WMAP and Planck experimentation and analysis of data in order to find if these maps are a caused by something local like a Doppler Shift or if it is indeed a valid component of the CMB. After all the analysis there is little doubt that this is indeed related to large scale anisotropies in the very early universe. Some have hinted towards new physics as being the cause for these large scale anisotropies. [101]
One such kind of anisotropy is rotation. But the evidence that directly links it to rotation and shows that these anisotropies are in fact a global phenomena comes from the fantastic and brilliant work of Lior Shamir of Kansas State University and his paper from last year: Multipole alignment in the large-scale distribution of spin direction of spiral galaxies. [102]

The spiral arms of a galaxy when viewed from Earth can be seen to have a clockwise or anti-clockwise spin. Starting from the centre and moving out the spiral patterns on the left show clockwise spiral. The spirals on the right, starting from the centre and moving out, show an anti-clockwise spiral.
The rotation of a given spiral galaxy can be either rotating clockwise or anti-clockwise. We can see a symbolical representation of this binary in that a spiral galaxy is either spinning in a clockwise direction or an anti-clockwise direction in the artwork which helps refine my ideas. The spirals on the left has a clockwise rotation when starting from the centre and working outwards. The spirals on the right has an anti-clockwise rotation when starting from the centre and working outwards.
A nice pair of hairy bollocks; maybe that’s what the original artist actually got nailed up for. Off course, please you’ll have to forgive my humour. Laughter is my only defence mechanism I have in keeping my humanity alive and in check less it get swept away in a tsunami of egotistical fate. I just learnt a long time ago now never to take either myself or my religion too seriously.
In his paper Lior Shamir describes the computer visualisation algorithm that he developed in order to determine if a spiral galaxy is rotating either clockwise or anti-clockwise. Using datasets from Pan-STARRS and SDSS of images of spiral galaxies he employed his algorithm to find their respective direction of rotation. With the SDSS dataset he identified 88,273 galaxies with clockwise spin patterns and 86,075 galaxies with anti-clockwise spin patterns. From the Pan-STARRS dataset he identified 16,508 galaxies with a clockwise spin direction and 16,520 galaxies with an anti-clockwise spin.
Given the cosmological principle of isotropy then the expected result is that overall spiral galaxies should have no preferred direction of rotation. So if I were to randomly select an area of the night sky, upon the celestial sphere, and count the number spiral galaxies both with clockwise and anti-clockwise rotation then I would expect a 50:50 split in terms of probability; given that the number of spiral galaxies sampled is of a sufficiently large enough size. Effectively there should be no asymmetry between the different spin of spiral galaxies.
What Lior showed was that this was not the case. Rather the split was found to be 49:51 in favour of clockwise rotation in some parts of the sky and 51:49 split in other parts of the sky.
The quadruple map show a measurement of probability, denoted as \(\sigma\), in there being asymmetry between the observed clockwise and anti-clockwise galaxy spinward direction. Or more specifically, the probability of quadruple alignment in different \((\alpha,\delta)\) combinations for a given dataset. The higher the value of \(\sigma\) the greater the asymmetry. The quadruple map on the left shows the Pan-STARRS dataset and on the right the SDSS dataset.
Where things get extremely interesting is in the resultant quadrupole map showing \(\sigma\); the probability of quadrupole alignment happening by chance. To quote, “The highest probability was achieved when fitting the distribution of galaxy spin directions to quadrupole, with probability greater than \(6\sigma\)”. Effectively showing that the asymmetry in the preferred rotation of galaxies is way beyond any mere coincidence.
But it is in how this specific quadrupole map shows the exact same lobe structure, in the same locations, as the quadrupole map showing the CMB temperature variation. Specifically there are four lobes in both maps. The regions inside the lobes corresponding to higher asymmetry are within the red/blue coloured regions of the map. While those regions showing symmetry in rotational spin are in the yellow/orange coloured regions of the map. The regions with the higher asymmetry correspond to the lobes of the CMB showing the highest temperature variation from the average.
Animated comparison between the quadruple map of the CMB and the two galaxy spin asymmetry quadruple maps.
Here for the first time is effective and convincing evidence that the large scale anisotropies on the quadrupole map of the CMB is most certainly linked to rotation. Specifically in this case the asymmetry in the rotation of spiral galaxies. To quote Shamir in conclusion “Since the spin patterns of a galaxy as visible from Earth is also an indication of the actual spin direction of the galaxy, the large scale spin directions can be an indication of a rotating universe”. [102]
On its own this is certainly a very significant result and has come as a surprise to most cosmologist. For my case, this is absolutely critical in showing that at the largest scale rotation was present in the Big Bang event.
But this next result for me effectively allows me to show the validity of the Big Bang Hypernova Hypothesis based on the primary evidence; the CMB.
Before we do let us imagine how the Big Bang Hypernova should appear in the large scale anisotropies of the CMB. The solution, as we have seen, is that our universe was born from a white hole. As described in the name Jet-a-verse our universe is effectively shaped as one of two jets arising from this S(1) Black Hole into a S(0) White Hole.
Also we have seen that the equations describing perfect fluid flow are also exact solutions of Einstein Field Equations. This is more accurately seen in using fluid vortex experiments as an analog to rotating black holes. A white hole, as we have also seen, is simply a time reversed black hole. Putting this together the shape of our early universe is a time-reversed vortex. [40] [86]
A streamline in a vortex can be characterised as a spiral. The curvature of a spiral increases the closer one gets to its central focal point. As an example the graph, on the left, shows an Archimedean spiral in red as defined by the cartesian equation \((a\theta cos(\theta),a\theta sin(\theta))\). The curvature is shown in blue which is defined by the equation: $$ \kappa = \frac{\theta^2+2}{a(\theta^2+1)^\frac{3}{2}} $$ As \(\theta\rightarrow0\) the value of the curvature rises to a maximum as the spiral circles in on its central focal point at \((0,0)\). So the pattern we are looking for is increased spiral curvature on the expected focal point. Note that this pattern is again seen echoed in the Archimedean spiral upon the provided inspirational artwork.
The characteristic streamline of flow into a vortex, when viewed from above, is a spiral that spirals down into the vortex ending in a central focal point. The curvature of a spiral increases the closer one is to the central point. This can be seen in the Archimedean spiral example above. The spiral is defined by the equation:
$$ (x(\theta),y(\theta))=(a\theta cos(\theta),a\theta sin(\theta))\phantom{xxxxxxxxx}(11) $$
Where \(\theta\) is a parametric parameter and is \(a\) is a fixed constant. In the illustrated example \(a=0.5\). The curvature of an Archimedean spiral is derived to be:
$$ \kappa = \frac{\theta^2+2}{a(\theta^2+1)^\frac{3}{2}}\phantom{xxxxxxxxx}(12) $$
The blue line in the graph above shows a plot of the curvature with \(\theta\) on the x-axis and \(\kappa\) on the y-axis. We see that the curvature of the Archimedean spiral rises to a maximum value of 4 as \(\theta\) approaches the central focal point of the spiral located at \((0,0)\).
So in thinking about the microwave sky we are looking for a spiral shaped anisotropy arising from a central location. In previous work, I have argued that this central location is the Cold Spot on the Cosmic Microwave Background (CMB) Sky. The Cold Spot is also known as the Eridanus Supervoid because it is reasoned that as temperature correlates to density of matter in the early universe it is a volume devoid of matter itself being significantly cooler in comparison to the rest of the CMB.
In my previous work I argue that the reason for their being a void is that it is the space that opens up between the location of the Big Bang Hypernova event and the end of the jet. There is only a finite amount of matter that fell into the S(1) black hole and thus became matter in our own universe via the adjoining S(0) white hole. So once all the matter that forms the inside of our Jet-a-verse has been ejected from the S(1) white hole then a volume of nothingness opens up as we begin to traverse the volume of the Superverse.
Particle animation of model that focuses on the initial jet formation and the subsequent void that develops as the jet moves away. In this model we add an additional point force field to act as the explosive force of the supernovae event. This is particularly to demonstrate how a supervoid can develop at the end of the jet’s formation. You can download the Blender model file by clicking this link.
Note as the jet moves away from the epicentre of the hypernova a void begins to open up. At the tale end of the jet a spherical void forms from how the particles are swept around at the tale end. Then another bubble shaped void forms in sequence. Then another bubble void forms in sequence.
This behaviour is captured in my first computational model in which I render the spherical volume at its fixed location. Another very particular pattern in this model which I want to point out is look at how the end of the jet is swept around and around. It creates a twisting corkscrew pattern in which a series of bubble voids form.
In this paper “Cosmic Troublemakers: the Cold Spot, the Eridanus Supervoid, and the Great Walls” by András Kovács, Juan García-Bellido. To quote from their abstract “Our tomographic imaging reveals important substructure in the Eridanus supervoid, with a potential interpretation of a long, fully connected system of voids.” A series of bubble voids. [103]
So we have our central focal point located in the middle of the Cold Spot upon the CMB. Thus we would expect that the anisotropies to have the greatest amount of curvature in the areas surrounding the Cold Spot upon the CMB. So if our universe was born from a white hole then because of the time-reversed vortex nature of ejection the central focal point of said vortex should be located centrally upon the Cold Spot of the CMB.
The Jet-a-verse also has a specific direction of travel; or rather overall, on average, a particular direction. Returning to the description given earlier where the expansion of our universe can be seen in fluidic terms. That is the perfect fluid solution of the FLWR-metric. I now raise the cosmological idea called dark flow.

The colored dots are clusters within one of four distance ranges, with redder colors indicating greater distance. Colored ellipses show the direction of bulk motion for the clusters of the corresponding color. Images of representative galaxy clusters in each distance slice are also shown. Credit: NASA/Goddard/A. Kashlinsky, et al. [104]
Yet another subject worthy of a future essay, as well that bubble voids paper I only just found, the idea of dark flow is that there is a non-random component to the direction in which galaxy superclusters travel. The idea was born from the observation that our local galaxy cluster and its larger supercluster are all moving in the same direction. The accepted explanation is that this is due to the gravitational pull towards the Shapley Supercluster and in turn towards the Great Attractor. This is an area in the northern hemisphere which is hard to observe because the gas and dust in the Milky Way galaxy obscures our view; but which is transparent in the near-infrared wavelength of light. [103]
The trouble for the Great Attractor is in trying to find enough mass such that it has sufficient gravitational pull as to actually exert sufficient pull upon our own local supercluster. But what we do know is that our supercluster and surrounding clusters are flowing in that direction. Thus the flow of galaxies around the Local Supervoid is not seen as being anything odd or against the isotropic principle.
Panoramic view of the entire near-infrared sky. The location of the Great Attractor is shown following the long blue arrow at bottom right.
So in effect I have an area of the sky that extends from the Equator and into the Northern Hemisphere that is in the direction of the Shapley Supercluster and which corresponds to the average direction of travel of our Jet-a-verse as a whole. Drawing a line from the Cold Spot to the region of the Great Attractor gives us a very rough central axis within our own Jet-a-verse.
Left image from computational model highlighting our location in the Jet-a-verse. Right image shows my best guess at the average direction of travel originating in the CMB Cold Spot and heading towards the Great Attractor. The two images show first the ESO Planck map highlighting the cold spot and then the panoramic view of the entire near-infrared sky. Our position is off from the central axis with the Great Attractor located near the equator. [105]
Having now identified a central axis of rotation and direction for our Jet-a-verse let us return back to the large scale anisotropies particularly in the context of rotation.
Cosmologists have considered the idea that at the largest scale rotation and vorticity could be factors. The idea was most famously given form by Kurt Gödel’s solution to Einstein’s Field Equations and the Gödel metric. Also Steven Hawking consider the idea in 1968 in this paper “On the Rotation of the Universe”. [106] [107]
In order to test various assumptions about the anisotropic nature of the microwave sky cosmologists developed Bianchi models of the universe. Developed by Luigi Bianchi who developed this class of cosmological models that are homogenous but not necessarily isotropic on spatial slices. A subclass of Bianchi models is the standard isotropic model of the FLRW metric which we discussed earlier. [108]
Best-fit Bianchi Type VII_h model testing anisotropy and rotation. To quote the title of the paper “Evidence of vorticity and shear at large angular scales in the WMAP data: a violation of cosmological isotropy?”. [111]
In order to study model universes where rotation is a component of the anisotropy Jason McEwen and colleagues developed a Bianchi Type VII_h model. In order to constrain their model such that they can find the best fit-parameters they used data from WMAP and its large scale anisotropies. [109] [110] [111]
The actual high resolution map as published by the ESA Planck team with the actual large-scale anisotropies highlighted. [105]
These large scale anisotropies are highlighted in this map published by the ESA Planck team. Now unlike the quadrupole or octopole map this multipole map shows the highest resolution of these large scale anisotropies. In particular the two key features that are highlighted. The first is this fundamental alignment with the Solar System’s elliptic plane nicknamed the “Axis of Evil”. The second feature highlighted is the location of the Cold Spot itself. [105] [112]
In analysis of finding the best fit Bianchi Type VII_h model to the WMAP data this map was produced. To quote the title of the paper “Evidence of vorticity and shear at large angular scales in the WMAP data: A violation of cosmological isotropy?”. [111]
Comparison of the best-fit Bianchi model with the actual ESA Planck map. Note how the anisotropies with the highest curvature is located in the area directly overlying the Cold Spot. As predicted by the Big Bang Hypernova Hypothesis. [105] [111]
Notice the cold spot with high curvature located in the area of the Cold Spot. Note also the corresponding hot spot with high curvature. This curvature is again modelled across the lower half of our ecliptic plane but with much less curvature. Running parallel to this is another streamline of cold curvature on the northern side of the ecliptic plane. Run an arrow from the Cold Spot up to the location of the Great Attractor and we have the main direction of our Jet-a-verse.
Comparison of the best-fit Bianchi model with the actual ESA Planck map with arrows overlaid showing the curvature of the anisotropies. Note the anisotropies with the greatest amount of curvature is located around the Cold Spot. This shows a central vortex structure emanating from the centre of the Cold Spot: the S(0) white hole that gave birth to our universe. [105] [111]
Super-imposing the two maps we can see how a best-fit model that accounts for rotation of the universe shows a vortex structure centred on the Cold Spot. Given what I have said about the Higgs field as dictating the flow I reckon we have found a very reasonable explanation as to why our Solar System is aligned with this structure. This is what we would expect given that our universe was born from a time-reversed vortex such as a white hole. Not only that it corresponds to the exact location, the Cold Spot, where in previous work I have shown as being the epicentre for the Big Bang event.
Coupled to this that we know from Lior Shamir’s work these large scale anisotropies are linked to the preferred rotation of spiral galaxies. [102]
And so, from my point of view as the progenitor of the Big Bang Hypernova Hypothesis this for me is more or less victory. I not only have my smoking gun in terms of the Cold Spot but I also have the rifling from the bullet in the large scale anisotropies. This is the primary evidence coming from the Big Bang event itself matching the most simplest of explanations:
Fractal geometry is the cosmological principle thus self-similar patterns repeat themselves irrespective of scale. Following the pattern of a hypernova we can infer behaviour of this most explosive of events inside our universe in order to understand the biggest of them all, the Big Bang.
That is the simplicity of the Big Bang Hypernova Hypothesis and this coupled with everything else I have assembled is simply check-mate to the Lambda-CDM model.
Victory!

But before going, as I have highlighted, the “new physics” comes in understanding the physics of conformal geometry. Why a field is born lies buried in the understanding of Gravitoelectromagnetism where Einstein’s Field Equations are coupled with Maxwell’s Equations. It is also seen in the X-17 particle experiment and in Martin Tajmar’s frame dragging in a lab. These two experiments alone are the greatest game changer in humanities history; I would dare to predict and fate does seem to be on my side. [44]
Lastly, a quick word from our sponsor.
This essay has been brought to you by the letter A and these scaled blocks. “A” is for Apollo in whose mind mine now resides. The scaled blocks the horizons of a rotating black hole in whose help the Big Bang Hypernova Hypothesis has been developed. Turns out the Holy Grail of Physics required the real Holy Grail; aka the most important archaeological artefact in New Testament Biblical Studies.
“A” is also for arse; as I realise this is all a figment of my imagination. But as one of the greatest philosopher’s of the last century once said “That would be ecumenical matter!”

References:
- [1] Stratigraphic modelling of turbidite prospects to reduce exploration risk - Dave Waltham, Stuart MacLean, Noah Jaffery, Valentina Zampetti
- [2] Penrose Diagrams - Andrew Hamilton (Colorado University)
- [3] It’s mindboggling!’: astronomers detect most powerful black-hole collision yet - Nature
- [4] NASA's Fermi Telescope Finds Giant Structure in our Galaxy - NASA
- [5] Fermi Bubbles - NASA Fermi Space Telescope
- [6] Spacetime Singularities - Roger Penrose, Dennis Lehmkuhl and Melvyn Bragg - Oxford Mathematics
- [7] Planck evidence for a closed Universe and a possible crisis for cosmology - Eleonora Di Valentino, Alessandro Melchiorri & Joseph Silk
- [8] A Flat Universe from High-Resolution Maps of the Cosmic Microwave Background Radiation : P. de Bernardis, P.A.R.Ade, J.J.Bock, J.R.Bond, J.Borrill, A.Boscaleri, K.Coble, B.P.Crill, G.De Gasperis, P.C.Farese, P.G.Ferreira1, K.Ganga, M.Giacometti, E.Hivon, V.V.Hristov, A.Iacoangeli, A.H.Jaffe, A.E.Lange, L.Martinis, S.Masi, P.Mason, P.D.Mauskopf, A.Melchiorri, L.Miglio, T.Montroy, C.B.Netterfield, E.Pascale, F.Piacentini, D.Pogosyan, S.Prunet, S.Rao, G.Romeo, J.E.Ruhl, F.Scaramuzzi, D.Sforna, N.Vittorio
- [9] The 1965 Penrose singularity theorem - José M. M. Senovilla, David Garfinkle
- [10] A limit on the variation of the speed of light arising from quantum gravity effects - A. A. Abdo, M. Ackermann, M. Ziegler - Nature
- [11] An intergalactic race in space and time - Nature
- [12] A Gamma Ray Race Through the Fabric of Space-Time Proves Einstein Right - Eliza Strickland (Discover)
- [13] Bekenstein-Hawking entropy - Jacob D. Bekenstein (2008), Scholarpedia, 3(10):7375
- [14] The metre is the SI unit of length - NPL
- [15] Eben Alexander: A Neurosurgeon's Journey through the Afterlife - Theosophical Society
- [16] DMT Models the Near-Death Experience - Christopher Timmermann, Leor Roseman, Luke Williams
- [17] What is the Steady State Hypothesis? - Matt Williams (Universe Today)
- [18] 'Einstein's Biggest Blunder' May Have Finally Been Fixed - Tim Childers (Live Science)
- [19] Nobel Prize for Discovery of accelerating universe mysterious origin still unknown - Kurt Riesselmann (Symmetry Magazine)
- [20] Schwarzschild Solution to Einstein’s General Relativity - Carson Blinn (Washington University)
- [21] The Schwarzschild Metric - UCSD Physics 110B (UC San Diego)
- [22] The Universe on the Other Side (of the Black Hole) - Infinity Plus One
- [23] Gravitational Collapse and Space-Time Singularities - Roger Penrose (Physical Review Letters)
- [24] The Nobel Prize in Physics 2020 - Royal Swedish Academy of Sciences
- [25] Profile: Fritz Zwicky's Extraordinary Vision - American Museum of Natural History
- [26] Meet the Woman Who Found the Most Useful Stars in the Universe - National Geographic
- [27] Stars orbiting the black hole at the heart of the Milky Way - European Southern Observatory
- [28] Astronomers Image Magnetic Fields at the Edge of M87’s Black Hole - Event Horizon Telescope
- [29] Analytic conformal compactification of Schwarzschild spacetime - Jakub Halacek and Tomas Ledvinka (University of Prague)
- [30] Violation of CP Invariance, C-Asymmetry, and Baryon Asymmetry of the Universe - A. D. Sakharov
- [31] Is the Big Bang a black hole? - Philip Gibbs, 1997 (Mathematics Department, University of California, Riverside)
- [32] Properties of expanding universes - Stephen Hawking (University of Cambridge)
- [33] The Revival of White Holes as Small Bangs - Alon Retter & Shlomo Heller
- [34] The primordial explosion of a false white hole from a 5D vacuum - Jose Edgar, Madriz Aguilar, Claudia Morenoand, Mauricio Bellini (Centro Universitario de Ciencias Exactas)
- [35] An ‘Interstellar’ Explainer: What Are Bulk Beings? - W. W. Norton & Company
- [36] RADIAL MOTION INTO AN EINSTEIN-ROSEN BRIDGE - Nikodem J. Poplawski (Department of Physics, Indiana University)
- [37] Every Black Hole Contains Another Universe? - National Geographic
- [38] Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics - Roy Kerr (September 1963, Physical Review Letters 11(5):237-238)
- [39] Spinning Black Holes - Crafoord Laureate 2016: Roy Kerr, University of Canterbury, Christchurch
- [40] Quantum Gravity Laboratory
- [41] Vortex analogue for the equatorial geometry of the Kerr black hole - Matt Visser, Silke Weinfurtner (University of Wellington)
- [42] Rotational superradiant scattering in a vortex flow - Theo Torres, Sam Patrick, Antonin Coutant, Maurício Richartz, Edmund W. Tedford & Silke Weinfurtner (Nature)
- [43] Light speed reduction to 17 metres per second in an ultracold atomic gas - Lene Vestergaard Hau, S.E.Harris, Zachary Dutton & Cyrus H. Behroozi (M.I.T.)
- [44] Search for Frame-Dragging-Like Signals Close to Spinning Superconductors - M. Tajmar, F. Plesescu, B. Seifert, R. Schnitzer, and I. Vasiljevich (Space Propulsion and Advanced Concepts, Austrian Research Centers)
- [45] Eric Laithwaite's Reality-Defying 1974 Lecture on Gyroscopes
- [46] NASA's Gravity Probe B Confirms Two Einstein Space-Time Theories - NASA
- [47] Extraction of Rotational Energy from a Black Hole - R. PENROSE & R. M. FLOYD (Nature Physical Science)
- [48] Extraction of Energy from a Black Hole - Daniel Nagasawa (Stanford University)
- [49] Conformal Cyclic Cosmology. Roger Penrose and Hannah Fry - Oxford Mathematics
- [50] The plot thickens for a hypothetical “X17” particle - CERN
- [51] Has a Hungarian physics lab found a fifth force of nature? - Edwin Cartlidge (Nature)
- [52] Generation of Waves by a Rotating Body - Zel'dovich (USSR Academy of Sciences)
- [53] The many faces of superradiance - Jacob D. Bekenstein and Marcelo Schiffer (Racah Institute of Physics, Hebrew University of Jerusalem)
- [54] The Kerr spacetime: A brief introduction - Matt Visser (School of Mathematics, Statistics, and Computer Science Victoria University of Wellington)
- [55] Stephen Hawking's PhD thesis, explained simply - James Geach (World Economic Forum)
- [56] A Modified FRW Metric to Explain the Cosmological Constant - Serkan Zorba (Department of Physics and Astronomy - Whittier College)
- [57] ΛCDM Model of Cosmology - Lambda Education (NASA)
- [58] Einstein's quest for a unified theory - APS Physics
- [59] The Brout-Englert-Higgs mechanism - CERN
- [60] The matter-antimatter asymmetry problem - CERN
- [61] Big Bang Expansion and the Fundamental Forces - R.Nave (Hyperphysics Georgia State University)
- [62] Roger Penrose - Is the Universe Fine-Tuned for Life and Mind? - Closer to Truth
- [63] What is the Universe Made Of? - WMAP (NASA)
- [64] What Exactly Is a Black Hole Event Horizon (and What Happens There)? - Charles Q. Choi (space.com)
- [65] Tibetan Cosmological Models - Connecticut State University
- [66] Caiaphas Ossuary Symbols Decoded - Yirmeyahu Ben-David
- [67] Star's motion around Milky Way's monster black hole proves Einstein right yet again - Mike Wall (space.com)
- [68] Atlas - CERN
- [69] Nobel Prize Winner Frank Wilczek: Fundamentals -- What Are The 10 Keys To Reality? - Dr Brian Keating
- [70] Shut Up and Calculate!? - Wolt (Not Even Wrong)
- [71] Concentric circles in WMAP data may provide evidence of violent pre-Big-Bang activity. V. G. Gurzadyan and R. Penrose
- [72] The First Measurement of a Black Hole Merger and What it means. - LIGO Scientific Collaboration
- [73] Cosmological models of the Universe with reversal of time's arrow - Andrei Sakharov
- [74] Violation of CP Invariance, C Asymmetry, and Baryon Asymmetry of the Universe - Andrei Sakharov
- [75] THE MISSING PRIMEVAL ANTIMATTER SAKHAROV'S TWIN UNIVERSE - Janus Cosmological Model (Jean-Pierre Petit)
- [76] A Gravitational Origin of the Arrows of Time - Julian Barbour, Tim Koslowski and Flavio Mercati
- [77] THE JANUS POINT, ENTROPY AND THE ARROW OF TIME - Janus Cosmological Model (Jean-Pierre Petit)
- [78] The Janus Point: A New Theory of Time - Julian Barbour
- [79] Twin Universes Cosmology - Jean-Pierre Petit
- [80] Polarizations of CMB and the Hubble tension - Noriaki Kitazawa (Department of Physics, Tokyo Metropolitan University)
- [81] When superfluids are a drag - David C. Roberts (Los Alamos National Laboratory)
- [82] Interaction between active particles and quantum vortices leading to Kelvin wave generation - Umberto Giuriato & Giorgio Krstulovic (Nature)
- [83] Extended Analysis of Gravitomagnetic Fields in Rotating Superconductors and Superfluids - M. Tajmar (CERN)
- [84] Evaluation of enhanced frame-dragging in the vicinity of a rotating niobium superconductor, liquid helium and a helium superfluid - Martin Tajmar
- [85] Cool horizons for entangled black holes - Juan Maldacena and Leonard Susskind
- [86] Exact solutions of Einstein's equations - Prof. Malcolm A.H. MacCallum (Queen Mary University of London)
- [87] First results from Fermilab’s Muon g-2 experiment strengthen evidence of new physics - Muon g-2 experiment (Fermilab)
- [88] Muon g-2 experiment finds strong evidence for new physics - Fermilab
- [89] Feynman’s wobbling plate - Slavomir Tuleja, Boris Gazovic, and Alexander Tomori (American Journal of Physics 75, 240)
- [90] First Flight of the Ingenuity Mars Helicopter: Live from Mission Control - NASA
- [91] Researchers reveal common origin of Fermi bubbles and galactic center X-ray outflows - Liu Jia, Chinese Academy of Sciences
- [92] SIMULATING THE FERMI BUBBLES AS FORWARD SHOCKS DRIVEN BY AGN JETS - Ruiyu Zhang and Fulai Guo (Shanghai Astronomical Observatory)
- [93] The wisdom of the Universe - Interview with Nassim Haramein (Anthony Chene production)
- [94] Quantum Gravity and the Holographic Mass - Nassim Haramein
- [95] How big is the proton? Particle-size puzzle leaps closer to resolution - Davide Castelvecchi (Nature)
- [96] THE M–σ AND M–L RELATIONS IN GALACTIC BULGES, AND DETERMINATIONS OF THEIR INTRINSIC SCATTER - KAYHAN GULTEKIN, DOUGLAS O. RICHSTONE, KARL GEBHARDT, TOD R. LAUER, SCOTT TREMAINE, M. C. ALLER5, RALF BENDER6, ALAN DRESSLER, S. M. FABER8, ALEXEI V. FILIPPENKO, RICHARD GREEN, LUIS C. HO, JOHN KORMENDY, JOHN MAGORRIAN, JASON PINKNEY, AND CHRISTOS SIOPIS
- [97] History of the CMB Dipole Anisotropy - Edward L. Wright (UCLA)
- [98] Cosmic Microwave Background Anisotropy - Edward L. Wright (UCLA)
- [99] On the large-angle anomalies of the microwave sky - Craig J. Copi⋆, Dragan Huterer, Dominik J. Schwarz and Glenn D. Starkman
- [100] A high resolution foreground cleaned CMB map from WMAP - Max Tegmark, Angelica de Oliveira-Costa & Andrew J. S. Hamilton
- [101] Does the small CMB quadrupole moment suggest new physics? - James M. Cline, Patrick Crotty, Julien Lesgourgues
- [102] Multipole alignment in the large-scale distribution of spin direction of spiral galaxies - Lior Shamir (Kansas State University)
- [103] Cosmic troublemakers: the Cold Spot, the Eridanus Supervoid, and the Great Walls - András Kovács, Juan García-Bellido
- [104] Mysterious Cosmic 'Dark Flow' Tracked Deeper into Universe - NASA/Goddard/A. Kashlinsky, et al.
- [105] Planck enhanced anomalies - Planck (ESA)
- [106] An Example of a New Type of Cosmological Solution of Einstein's Field Equations of Gravitation - Kurt Gödel (Princeton)
- [107] On the Rotation of the Universe - Stephen Hawking
- [108] Bianchi universes - Dr. Andrew Pontzen, University College London (Scholarpedia)
- [109] Is the Universe rotating? - Jason McEwen (University College London)
- [110] Bayesian analysis of anisotropic cosmologies: Bianchi VIIh and WMAP - J. D. McEwen, T. Josset, S. M. Feeney, H. V. Peiris1 and A. N. Lasenby (University College London)
- [111] Evidence of vorticity and shear at large angular scales in the WMAP data: a violation of cosmological isotropy? - T. R. Jaffe, A. J. Banday, H. K. Eriksen, K. M. Gorski, F. K. Hansen
- [112] That's odd: Axis of evil stretches across the cosmos - New Scientist